Kirchoff's Law

KIRCHOFF'S LAW

Kirchoff's current and voltage laws are used to systematically analyze the relationships between voltages and currents in a given electric circuit.

Kirchoff's Current Law (KCL)

Kirchoff's current law states that the algebraic sum of currents at any node is zero. That is the total current entering a node is equal to the total current leaving that node.

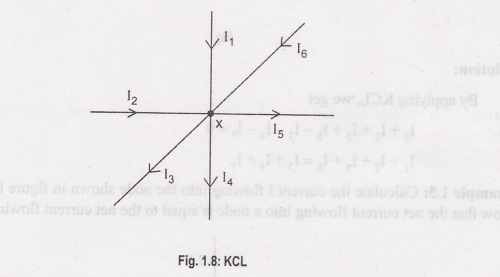
From Figure 1.8. There are three positive currents I, I, and I and three negative currents 13, 14, 15. Then according to Kirchoff's current law, The algebraic sum of the currents should be equal to zero.

If it is assumed that current entering the node has negative polarity and current leaving the node has positive polarity then KCL is written as:

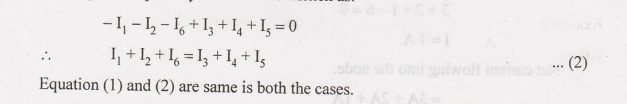
Equation (1) and (2) are same is both the cases.

Example 1.4: Write the equation for the current at the node shown in the figure below

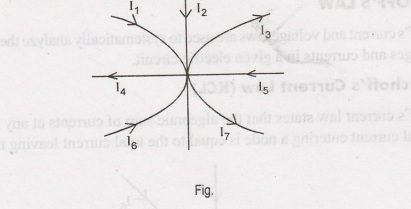
Solution:

By applying KCL, we get

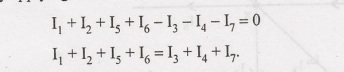
Example 1.5: Calculate the current I flowing into the node shown in figure below. Also show that the net current flowing into a node is equal to the net current flowing out of it,

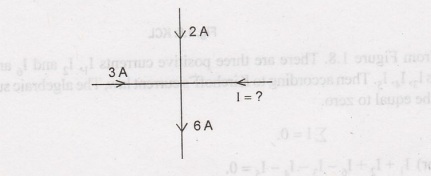
Solution:

Consider the current flowing toward the node as positive currents and leaving the nodes as negative currents. Applying KCL we get

Example 1.6: For the circuit shown below calculate the value of current

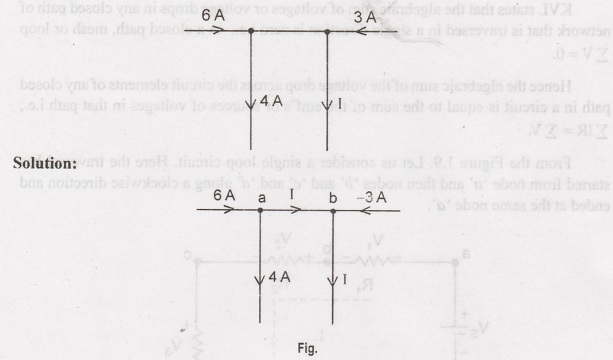
Two separate nodes 'a' and 'b' can be merged into a single super node c is shown in figure below.

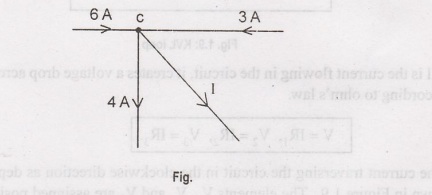
Applying KCL to super-node 'c' we get

6-3=4+I.

Therefore I = -1 A.

The negative sign in the result shows that the actual direction of the flow of current I is opposite to the direction of flow of current as shown in figure.

Kirchoff's Voltage Law (KVL)

KVL states that the algebraic sum of voltages or voltage drops in any closed path of network that is traversed in a single direction is zero i.e., in a closed path, mesh or loop Σν = 0.

Hence the algebraic sum of the voltage drop across the circuit elements of any closed path in a circuit is equal to the sum of the emf's or sources of voltages in that path i.e., ΣIR = ΣV.

From the Figure 1.9. Let us consider a single loop circuit. Here the traversal has started from node 'a' and then nodes 'b' and 'c' and 'd' along a clockwise direction and ended at the same node 'a'.

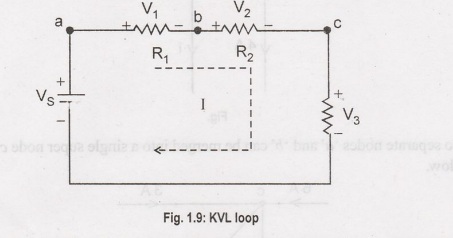
If I is the current flowing in the circuit, it creates a voltage drop across each resistor. Then according to ohm's law.

V=IR₁, V₂ = IR₂, V₃ = IR₃.

The current traversing the circuit in the clockwise direction as depicted by dashed line shown in Figure 1.9. The elements V₁, V₂ and V₃ are assigned positive sign and its positive a polarity is met first in the assumed traverse direction. Similarly Vs is assigned negative sign as its negative terminal is met first in the assumed traverse direction. The starting point of the loop is entirely arbitrary but it must start and end at the same point.

By applying KVL through the direction a -b -c -d - a we get

V₁+V₂+V₃ - Vs=0

Example 1.7: Determine the value of unknown voltage drop VR for the circuit shown below:

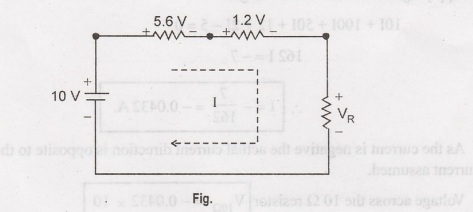
Solution:

Applying KVL we get

5.6+1.2+VR - 10 = 0

V_R = 3.2 V.

Example 1.8: For the circuit shown below find the circuit current and voltage across the 10 Ω  resistor.

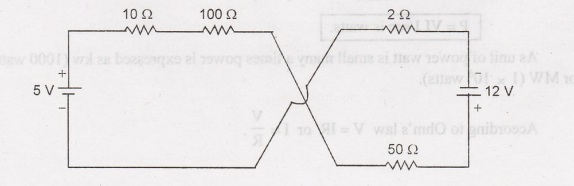
Solution: The circuit can be re-arranged as:

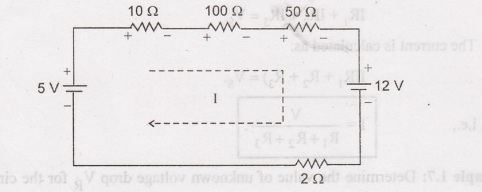
Applying KVL to the circuit we get:

101 +1001+501 + 12+ 21-5=0.3

162 I=-7

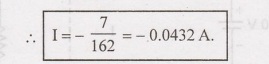
As the current is negative the actual current direction is opposite to the direction of the current assumed.

Voltage across the 10 2 resistor