Generation Of AC Voltage

GENERATION OF AC VOLTAGE

The machines which are used to generate electrical voltages are called generators. The generators which generate pure sinusoidal a.c voltage waveforms are called as alternators.

The basic principle of an alternator is the principle of electromagnetic induction. The sine wave is generated according to Faraday's law of electromagnetic induction.

Emf induced for different situations:

(i) Moving the conductor across the lines of force.

In this case maximum flux lines will be cuts by the conductor.

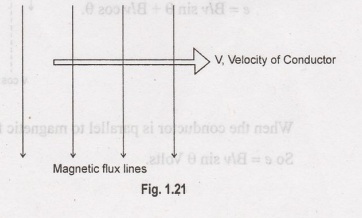
where

e → induced emf (v)

B→ flux density (ob/m²)

1 → length of conductor (m)

v → velocity of conductor (m/sec).

(ii) Moving the conductor parallel to the lines of force.

In this case, no flux lines will cut the conductor.

So e = 0 v.

(iii) Moving the conductor in such a way making an angle 'θ' with the lines of force.

In this case, velocity (v) can be resolved into two components.

 (i) Across the magnetic

flux = v sin θ

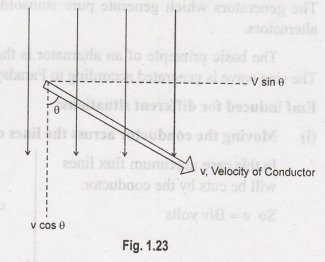
When the conductor is parallel to magnetic flux line e = 0.

So e = Blv sin 0 Volts.

Equation of an Alternating Quantity

To derive the equation of an ac quantity, consider single turn, 2 pole alternator. Th coil is rotated with constant angular velocity in the magnetic fields.

An alternating emf induced is purely sinusoidal in nature.

Let B → Flux density of the magnetic field in ob/m²

1 → Active length of each conductor in metres

r→ Radius of circular path traced by conductors in metres

ω→ Angular velocity of coil in radians/second

v → Linear velocity of conductor in m/sec.

Now v=rω.

Consider an instant where coil has rotated through angle corresponding to θ=θ° i.e., from the instant when induced emf is zero.

If requires time 't' to rotate through 0. So e in radians can be expressed as: 0 =

θ= wt radians.

The position of coil is shown in Figure 1.24(a). The instantaneous peripheral velocity of any conductor can be resolved into two components as shown in Figure 1.24(b).

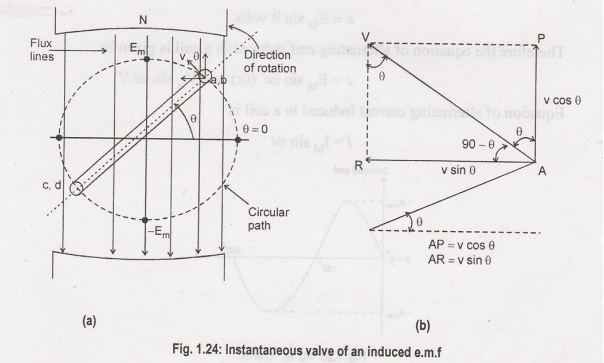
The components of velocity, vare:

(1) Parallel to the magnetic flux lines

(2) Perpendicular to the magnetic flux lines = v sin θ.

Out of the two, due to the component parallel to the flux, the component parallel to the flux, there cannot be the gene of the e.m.f as there cannot be the cutting of the flux lines. Hence the component which is acting perpendicular to the magnetic flux lines.

According to the Faraday's law electromagnetic induction, the expression for the  generated emf in each conductor is:

The active length 'l' means the length of the conductor which is under the influence of the magnetic field.

Now E_m = Blv

= maximum valve of induced emf in conductor.

This is achieved at θ = 90° and is the peak value or amplitude of the sinusoidal induced emf.

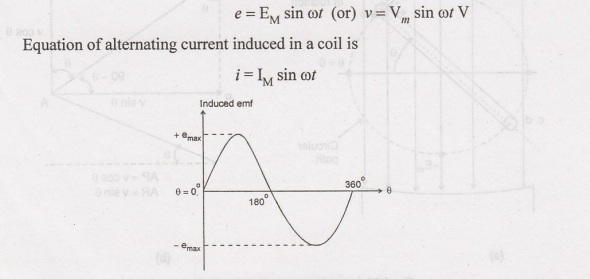
Hence the equation giving instantaneous valve of the generated e.m.f can be expressed as

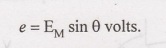
Therefore the equation of alternating emf induced in a coil is given by: