Transforms And Partial Differential Equations: UNIT V: Z - Transforms And Difference Equations

Worked Examples

Home | Department: Mech Department | Subject: Transforms and Partial Differential Equations |

<< Previous

Next >>

Transforms And Partial Differential Equations: UNIT V: Z - Transforms And Difference Equations: Worked Examples

WORKED EXAMPLES

(1) Find the Z-transform and region of convergence of

Hence Z [u (n)] is convergent if z lies between the annulus as shown shaded in figure. Hence, ROC is 2 <z < 4.

(2) Find the Z-transform and region of convergence of

u (n) = ⁿC_k, n ≥k

This series is convergence for | 1/z | < 1 i.e., for z> 1.

Hence ROC is ❘z❘> 1.

(3) Find Z-1 {(z − 5)⁻³] when ❘z❘ > 5. Determine the region of convergence.

Solution :

The region of convergence is the exterior of the circle |z❘ = 5 i.e., with centre at origin and of radius 5.

(4) Find the Z-transform and the radius of convergence of u (n) = 2ⁿ, n < 0

Solution :

Let u (n) = 0 for n ≥ 0 we have

(5) Find the Z-transform and the radius of convergence of

Solution :

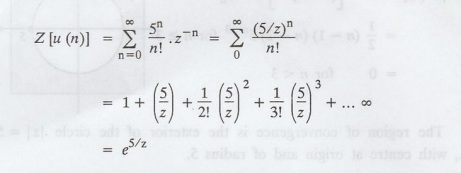
The above series is convergent for all values of z.

Hence, ROC is the entire z-plane.

Transforms And Partial Differential Equations: UNIT V: Z - Transforms And Difference Equations : Tag: : - Worked Examples

Home | Department: Mech Department | Subject: Transforms and Partial Differential Equations |

<< Previous

Next >>

Transforms And Partial Differential Equations: UNIT V: Z - Transforms And Difference Equations

Introduction

Problems based on Z-transform of some basic functions - Examples

Inverse Z-Transform - Methods

Convolution Theorem - Definition

Formation Of Difference Equations

Solution Of Difference Equations Using Z-transform

Exercise - Solution of difference equations using Z-transform.

Miscellaneous Problems

Convergence Of Z-Transforms

Worked Examples

Exercise - Convergence Of Z-Transforms

Questions And Answers

Under Subject

Transforms and Partial Differential Equations

MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation

Related Subjects

Transforms and Partial Differential Equations

MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation

Engineering Mechanics

ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation

Engineering Thermodynamics

ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation

Fluid Mechanics and Machinery

CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation

Engineering Materials and Metallurgy

ME3392 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation

Manufacturing Processes

ME3393 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation