Transforms And Partial Differential Equations: UNIT V: Z - Transforms And Difference Equations
Problems based on Z-transform of some basic functions
Examples
Transforms And Partial Differential Equations: UNIT V: Z - Transforms And Difference Equations: Examples
I. problems based on Z-transform of some
basic functions
Find
the Z-transform of the following functions:
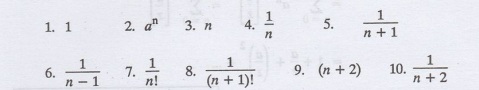
1.
Prove that, Z [1] = z/-1, z > 1,
Solution: We know that, Zx (n)}z
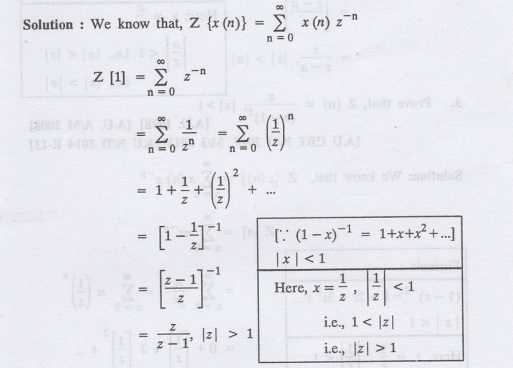





Linearity property:
 The Z-transform is linear
The Z-transform is linear
(i.e.,) Z {ax (n) + by (n)} = a Z {x (n)} + b
Z {y (n)}
II. Problems based on Z (1) = z/z-1 and Z
[an] z /z-a if |z| > |a|
Find
the Z-transform of the following functions:
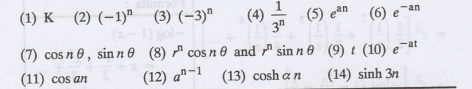
1.
Find Z (K)
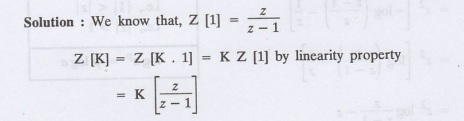
2.
Find Z [(-1)"]
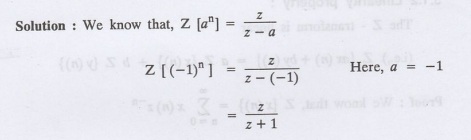
3.
Find Z [(-3)"]
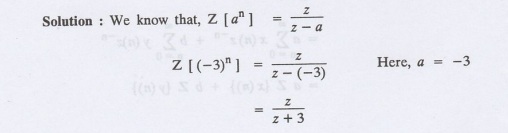
4.
Find Z[1/3n]
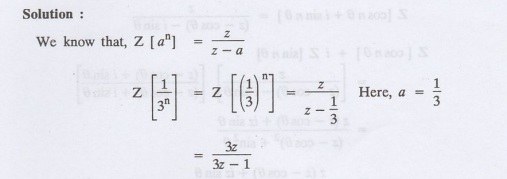
5.
Find Z [ean]
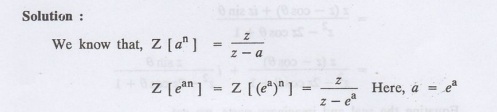
6.
Find Z [e-an]
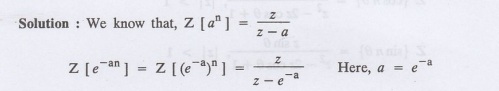
7.
Find Z [cos nθ] and Z d Z [sin nθ]

8.
Find Z [rncos nθ] and Z [rn sinθ ]

9.
Find Z (t).
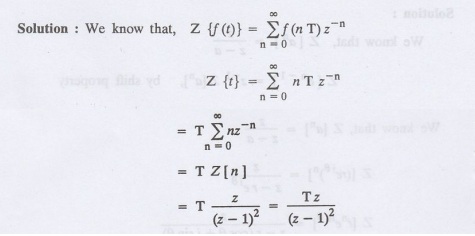
10.
Find Z [e-at]
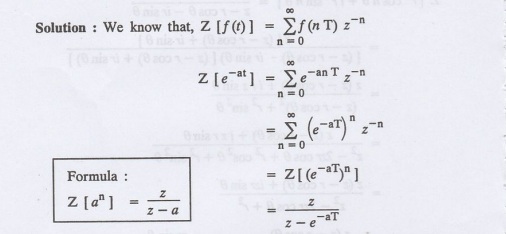
11.
Find Z [cos an]
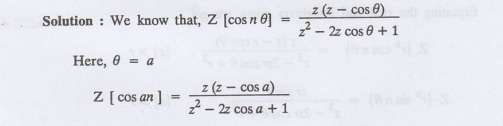
12.
Find Z [an-1]
Solution
:
We know that, Z [an]
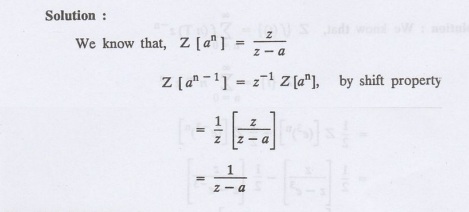
13.
Find Z [cosh a n]
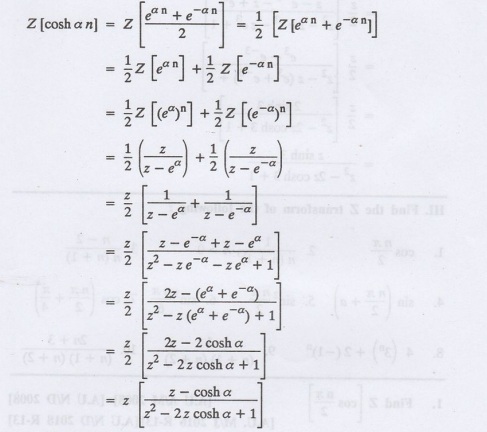
14.
Find Z [sinh 3n]

III. Find the Z transform of the following:
1.
Find Z [cos n π/2]

2.
Find Z [1/n (n + 1)]

3.
Find Z [n-2/n (n + 1)]

4.
Find 2 [sin(n π /2+a)]

5.
(a) Find [sin2 nπ /2]

5.
(b) Find Z [sin2 nπ /4]
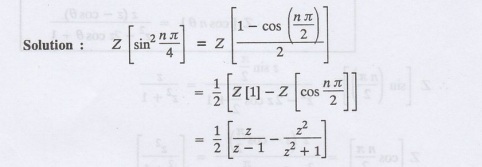
6.
Find Z [sin3 (nπ /6)]


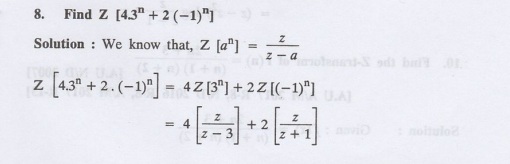
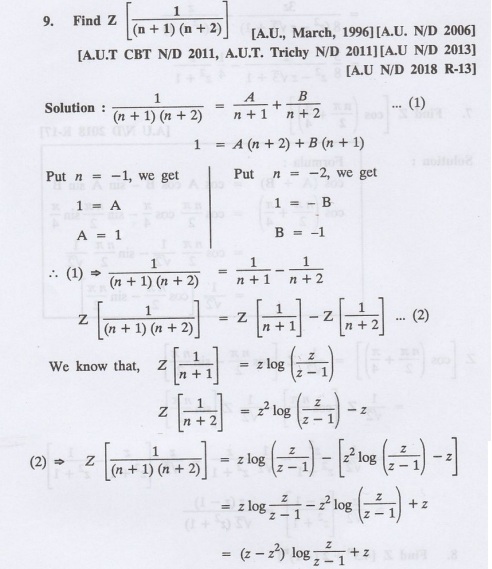

Differentiation in the Z-Domain

IV.
Find the Z-transform of the following:
[Differentiation
in the Z-Domain]
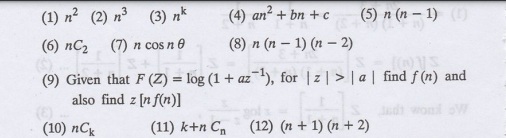
1.
Find Z (n2)
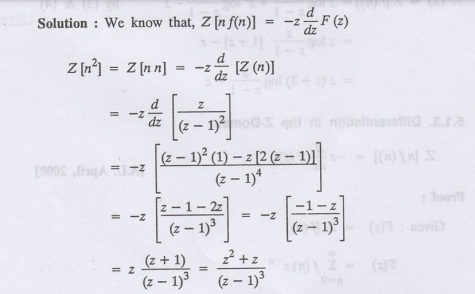
2.
Find Z (n3)
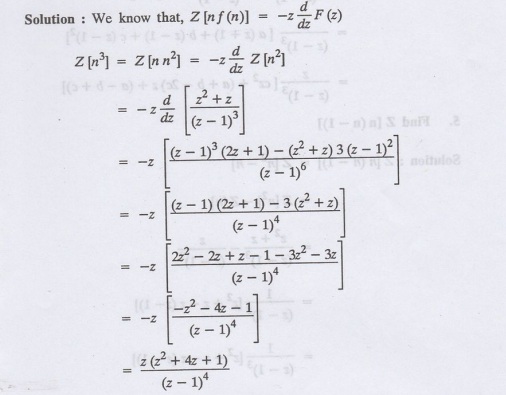
3.
Find Z (nk)
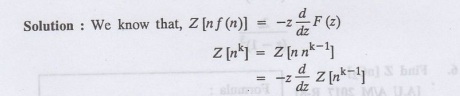
Which is a recurrence formula.
4.
Find Z [an2 + bn + c]
Solution:
Z [an2 + bn + c]
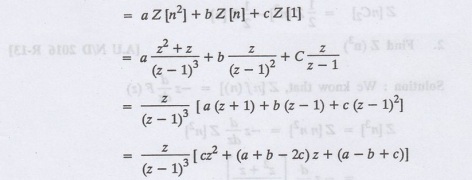
5.
Find Z [n (n-1)]
Solution:
Z [n (n − 1)] == Z [n2-n]
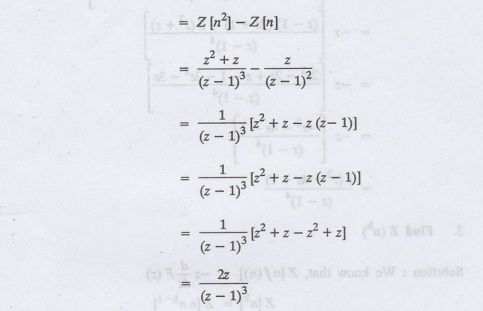
6.
Find Z [nC2]


8.
Find Z [n (n - 1) (n = 2)]

9.
Given that F (z) = log (1 + az-1), for |z| > |a |, find f(n) and also
find Z[n f(n)].
Solution:
Given : F(z) = log (1+ az -1)

10.
Find the Z-transform of {nCk}.
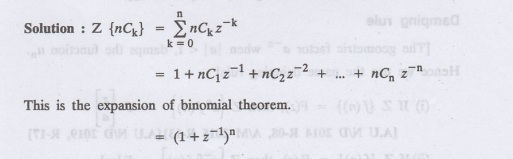
11.
Find the Z-transform of {k+n C2}
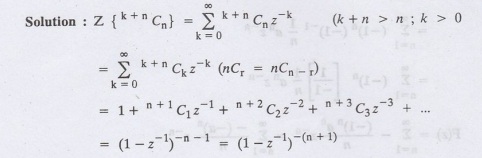
12.
Find the Z-transform of (n + 1) (n + 2).
Solution:
Z[(n + 1) (n + 2) ] = Z [n2 + 2n + n + 2]

First Shifting theorem [Frequency
shifting]:
Damping
rule
[The geometric factor a-n
when a < 1, damps the function un Hence we use the name damping
rule]

V. Problems based on first shifting theorem
[Frequency shifting]
Find
the Z-transform of the following:
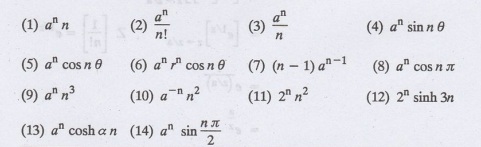
1.
Find Z [a" n]
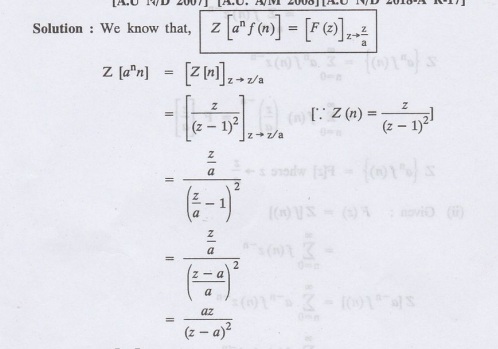
2
Find Z [an/n!]
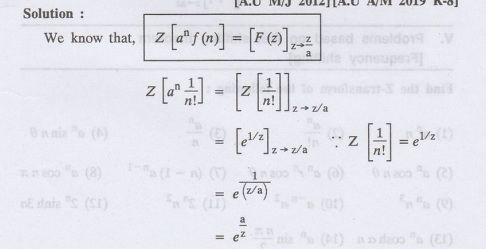
3.Find
[an/n]

4.
Find Z [an sin nθ ]
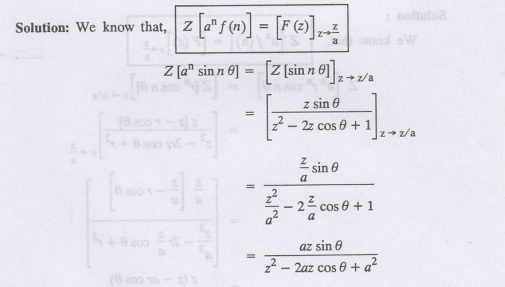
5.
Find Z [an cos nθ]
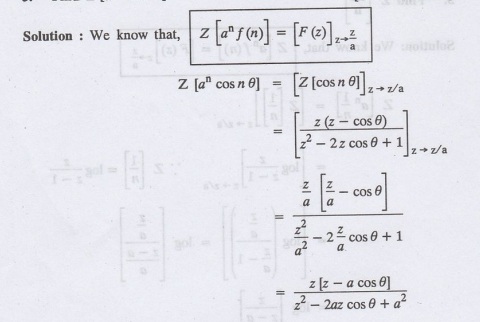
6.
to Find Z [an rn cos nθ]

7.
Find Z [(n-1) an-1]
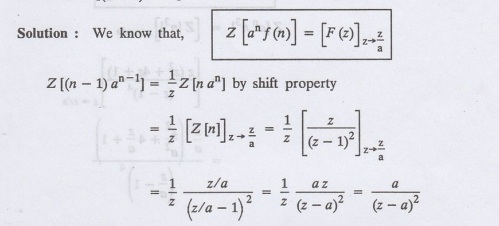
8. Find Z [an cos n л]

9. Find Z [an n3]

10.
Find Z[a-n n2]
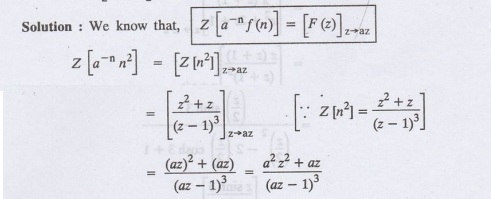
11.
Find Z [2n
n2]
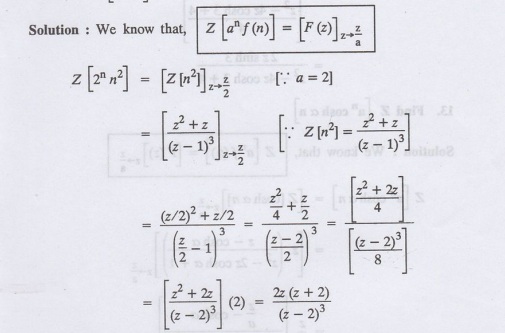
12.
Find Z [2n sinh 3n]

13.
Find Z [an cosh a n]

14.
(i) Find Za" sin

Second shifting theorem [Time Shifting]

VI. Problems based on Time shifting
Find
the Z-transform of the following:

1.
Find Z [1/(n + 2)!]
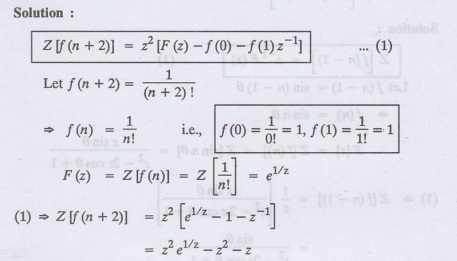
2.Find
Z [cos (n + 1) θ]

3.
Find Z [sin (n-1)θ]
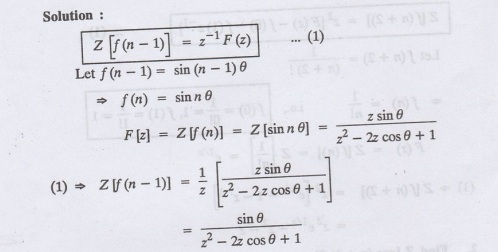
Unit impulse sequence
and unit step sequence.
Definition:
Unit impulse sequence
The unit impulse
sequence 8 (n) is defined as the sequence with values
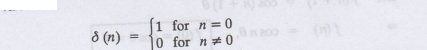
(1)
Z-Transfrom of unit impulse sequence is 1. i.e., Z [δ (n)] = 1
 P
P
(2)
Z-transform of unit step sequence i.e., Z (u (n)} = z/Z-1
Proof
:
We know that,
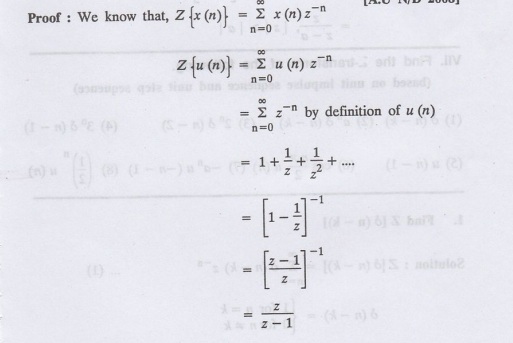

VII. Find the 2-transform of the following.
(based
on unit impulse sequence and unit step sequence)
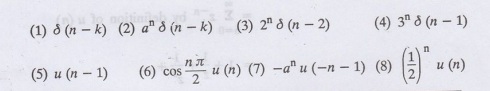
1.
Find Z [δ (n-k)]
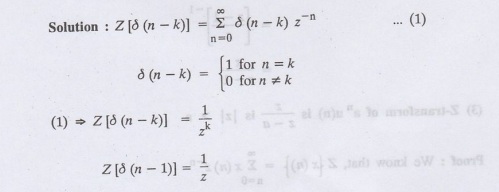
2.
Find Z [an δ (n − k)]
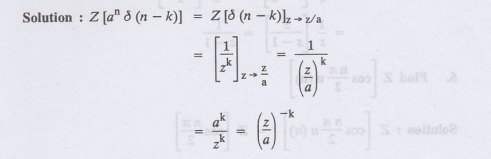
3.
Find Z [2n δ (n-2)]
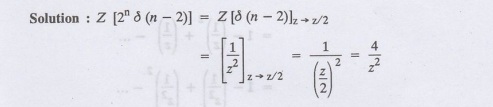
4.
Find Z [3n δ (n − 1)]
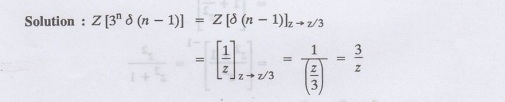
5.
Find Z [u (n-1)]
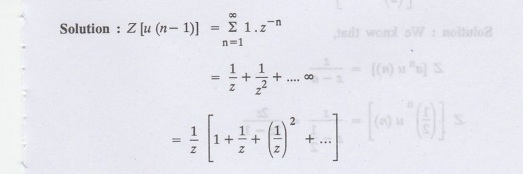

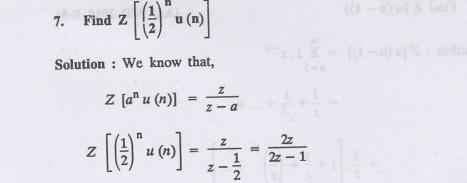
Initial value theorem and final value theorem.
1.
Initial value theorem
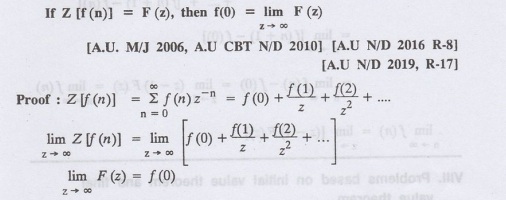

VIII. Problems based on initial value theorem and final value
theorem





Differentiation:
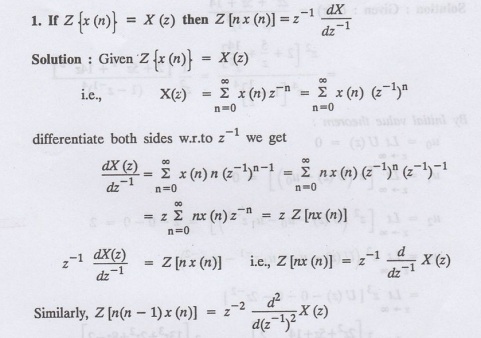
IX. Problems based on
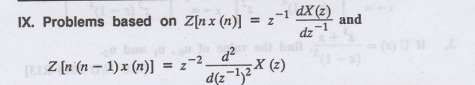

Transforms And Partial Differential Equations: UNIT V: Z - Transforms And Difference Equations : Tag: : Examples - Problems based on Z-transform of some basic functions
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
