Hydraulics of Pipe Lines

HYDRAULICS OF PIPE LINES

(i) The bed of pressure conduits should be as far as possible near HGL (Hydraulic M (ii) atibo gradient line).

Otherwise the increased pressure in pipes necessitates thicker and stronger pipes which will increase the cost.

(ii) Hydraulic Gradient Line should generate sufficient velocities. The velocity should be non silting / non-scouring. (0.9 m/s to 1.5 m/s)

(iii) Structural stability

(iv) Economical construction

(v) Head loss due to pipe friction.

(vi) Loss due to changes in flow geometry i.e., change in pipe size, bends, valves etc.

Head Loss formulae:

(i) Darcy-Weisbach formula (friction flow)

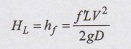
H_L =h_f = Head Loss due to pipe-friction in metres (m)

L = Length of pipe in m.

D = Diameter of pipe in m

V = Velocity of flow in m/s

f' = dimensionless friction factor

o = Acceleration due to gravity (9.81 m²/s)

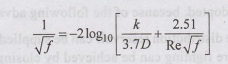
k = roughness projection (mm)

Re = Reynolds number

 

(ii) Manning's formula - For gravity conduits and turbulent flow in pressure conduit

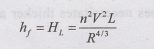
For circular pipe with full flow

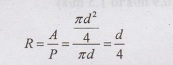
n = Manning's rugosity Coefficient.

L = Length of pipe in (m)

V = Flow velocity (m/s)

R = Hydraulic mean depth of pipe

 

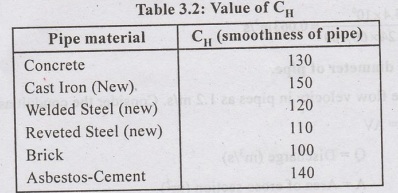
(iii) Hazen-William's formula

V = 0.85 C_H R^0.63 $^0.54

CH = Coefficient of hydraulic capacity (refer Table 2.3)

For Smoother pipe C_H is greater

R = Hydraulic mean depth of pipe in m.

For Circular pipe, R=d/4

S = Slope of energy line

Limitations of Hazen-william's formula

(i) The co-efficient C_H is not dimensionless. Its value varies.

(ii) C_H is independent of friction conditions (pipe diameter, viscosity, velocity, roughness and Reynold's number etc.)

Hence, Hazen William's gave a modified formula

 

Problem 3.1:

Determine the size of a supply conduit for serving a small town of population 25,000. Also find the hydraulic gradient at which the pipeline is proposed to be laid. Assume datas wherever required.

Solution:

Population = 25,000

Assume the average daily consumption of water (per capita demand) as = 120 /ped.

= Population × per capita demand

= 25,000 × 120 /ped

= 3 x 10⁶ l/d = 3 MLD

Maximum daily demand

= 1.8 x Average daily demand

= 1.8 x 3 MLD

= 5.4 MLD

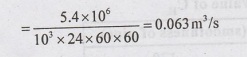
(a) To find the diameter of pipe.

Water Supply and Waste Water Engineering

Assume flow velocity in pipes as 1.2 m/s. Consider the conduit as circular.

Q = AV

Where,

Q = Discharge (m³/s)

A = Area of cross-section (m²)

V = flow velocity (m/s)

0.063 m³/s = A x 1.2 m/s

A = 0.063 / 1.2

A = 0.0525 m²

For circular conduit

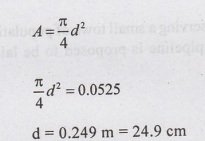
Provide 25 cm diameter pipe

 

(b) To find Hydraulic gradient?

Use Hazen-William's formula

Assume C_H = 110

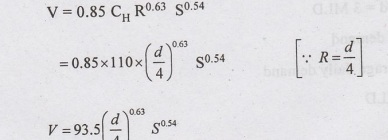
Problem 3.2:

In a water supply system to be designed for serving a population of 4 lakhs, the storage reservoir is situated at 8 km away from city and the loss of head from source to city is 16 meters. Calculate the size of supply main by using Weisbach formula as well as by using Hazen's formula assuming a maximum daily demand of 200 litres per day per person and half of the daily supply to be pumped in 8 hours. Assume coefficient of friction for the pipe material as 0.012 in Weisbach formula and CH = 130 in Hazen's formula

Solution:

Maximum daily per capita demand = 200 lpcd

Population = 4,00,000

Maximum daily water demand = Population x per capita demand

= 4,00,000 × 200 lpcd

= 80 × 10⁶ 1/d

= 80 MLD

Maximum water demand for which supply main is to be designed

80×24/2 × 1/8 = 80×12/8  MLD=120 MLD

(Since half the daily supply is pumped in 8 hrs)

Q=120 MLD: = 120×10⁶ /10³ × 24 × 60 × 60 m³/s=1.39m³/s

Now, Q = 1.39 m³/s, L = 8 km = 8000 m, H_L = 16m

 

(a) Using Darcy-Weisbach formula

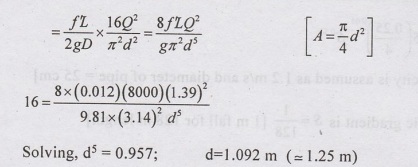
Use the nearest standard available pipe diameter (i.e. 1.25 metre diameter)

 

(b) Using Hazen-William's formula