Transforms And Partial Differential Equations: UNIT V: Z - Transforms And Difference Equations
Convolution Theorem
Definition
The convolution theorem plays an important role in the solution of difference equations and in probability problems involving sums of two independent random variables.
CONVOLUTION THEOREM
The convolution
theorem plays an important role in the solution of difference equations and in
probability problems involving sums of two independent random variables.
Definition:
Convolution of sequences :
1. The
convolution of two sequences
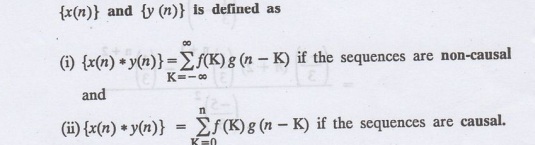
2. The
convolution of two functions f(t) and g(t) is defined as
State
and prove convolution theorem on Z-transform.
Statement
:
XI.
Z-transform of f (n) * g (n) type.
1.
Find the Z-transform of the convolution of
2.
Find the Z-transform of f(n) * g(n), where f(n) = u(n) and g(n) = δ(n) + (1/2) n
u(n).
Solution:
By convolution theorem,
3.
Find the Z-transform of f(n) * g(n) where f(n) g(n) = (1/2)n and g(n)
cos n л
Solution:
By convolution theorem,
XII.
Use convolution theorem to find the inverse Z-transform of
1(a)
Find Z-1 [z2/ (z-a) (z - b)
1(d)
Using convolution theorem evaluate inverse Z-transform of
Transforms And Partial Differential Equations: UNIT V: Z - Transforms And Difference Equations : Tag: : Definition - Convolution Theorem
Transforms And Partial Differential Equations: UNIT V: Z - Transforms And Difference Equations
Under Subject
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Materials and Metallurgy
ME3392 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Manufacturing Processes
ME3393 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation