Transforms And Partial Differential Equations: UNIT III: Application Of Partial Differential Equations
Steady State Solution Of Two Dimensional Equation Of Heat Conduction(Excluding Insulated Edges)
Introduction
When the heat flow is along curves, instead of straight lines, the curves lying in parallel planes, the flow is called two dimensional.
STEADY STATE SOLUTION OF TWO DIMENSIONAL
EQUATION OF HEAT CONDUCTION (EXCLUDING INSULATED EDGES)
TWO DIMENSIONAL HEAT FLOW EQUATIONS
Introduction
When the heat flow is along curves,
instead of straight lines, the curves lying in parallel planes, the flow is
called two dimensional.
The differential equation for two
dimensional heat flow for the unsteady case is
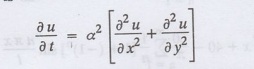
Here u (x, y) is the temperature at
any point (x, y) in time t, a2 is the diffusivity of the material.
Let us consider now the flow of
heat in a metal-plate in the xoy plane.
Let the plate be of uniform
thickness h, density p, thermal conductivity k and the specific heat c. Since
the flow is two dimensional, the temperature at point of the plate is
independent of the z co-ordinate.
The heat-flow lies in the xoy plane
and is zero along the direction normal to the xoy plane.
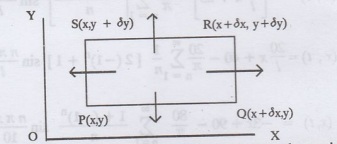
Now, consider a rectangular area
PQRS of the plate with sides dx and dy, the edges being parallel to the
co-ordinate axes, as shown in the figure.
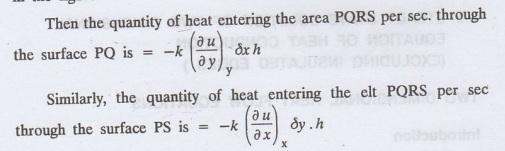 p
p
The amount of heat which flows out
through the surfaces QR and RS are
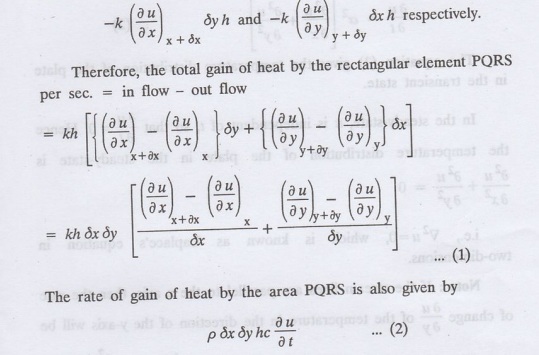
Equating the two-expressions for
gain of heat per sec from (1) and (2), we have
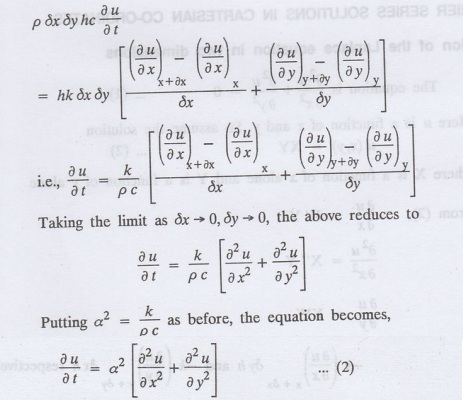
The equation (3) gives the
temperature distribution of the plate in the transient state.
In the steady-state, u is
independent of t, so that du/dt = 0 Hence the temperature distribution of the
plate in the steady-state is
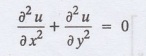
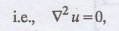 2u=0, which is
known as Laplace's equation in two-dimensions.
2u=0, which is
known as Laplace's equation in two-dimensions.
Note: If the stream lines are
parallel to the x axis, then the rate of change du/d of the temperature in the direction of the y-axis will be
zero. Then the heat-flow equation is reduced 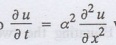 which is the heat-flow
equation in one-dimension.
which is the heat-flow
equation in one-dimension.
FOURIER
SERIES SOLUTIONS IN CARTESIAN CO-ORDINATES
Solution
of the Laplace equation in two dimensions
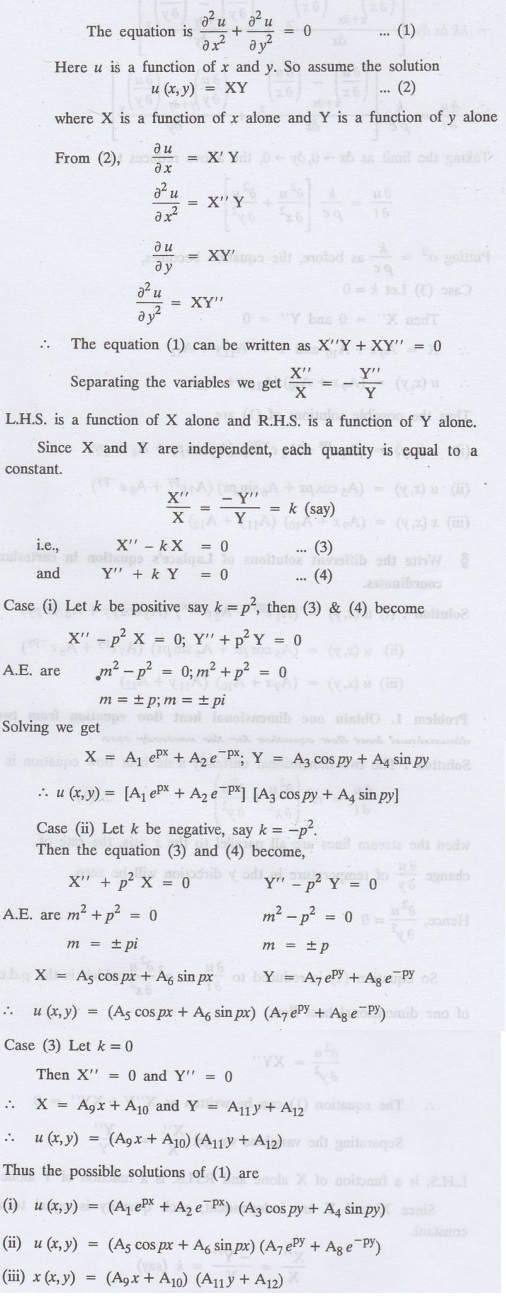
§
Write the different solutions of Laplace's equation in Cartesian coordinates.
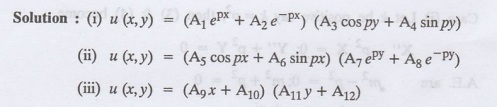
Problem
1. Obtain one dimensional heat flow equation from two dimensional heat flow
equation for the unsteady case.
Solution:
The two dimensional unsteady state heat flow equation is
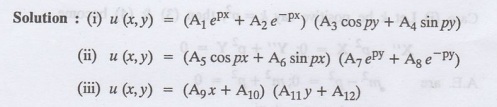
Problem
2. What is the equation to heat flow when the stream lines are non planar
curves?
Solution:
When the stream lines are non planar curves, the flow will be three dimensional
and the heat equation will be
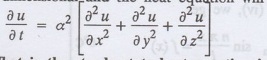
Problem
3.
What is the steady state heat equation in two dimensions in cartesian form?

Problem
4. Write down Laplace's equation in cartesian co-ordinates.
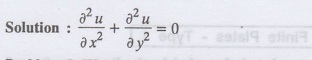
Problem
5. Write the three dimensional Laplace equation in cartesian form.
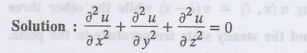
Note:
The two dimensional heat flow equation,
when steady state conditions exist is uxx + uyy = 0.
Type
1. Finite plate with value given in x direction :
Boundary conditions :
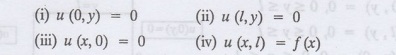
The suitable solution is given by
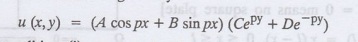
Apply condition (i), we get A = 0
Apply condition (ii), we get
Apply condition (iii), we get D =
-C
The most general solution is
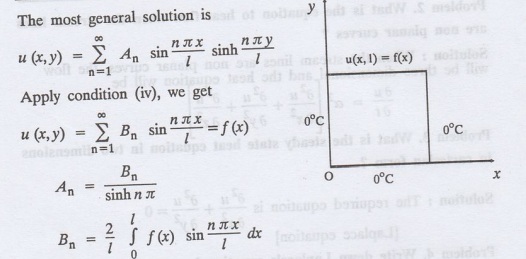
Transforms And Partial Differential Equations: UNIT III: Application Of Partial Differential Equations : Tag: : Introduction - Steady State Solution Of Two Dimensional Equation Of Heat Conduction(Excluding Insulated Edges)