Steady state conditions and zero boundary conditions

b. Steady state conditions and zero boundary conditions:

Problems based on Steady state conditions and zero boundary conditions

Example 3.4.b(1): What is meant by steady state condition in heat flow?

Solution: Steady state condition in heat flow means that the temperature at any point in the body does not vary with time.

i.e., it is independent of t, the time.

Example 3.4.b(2): In steady state conditions, derive the solution of one dimensional heat flow ?

Solution: The p.d.e. of unsteady one dimensional heat flow is

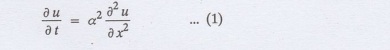
In steady state condition, the temperature u depends only on x and not time t

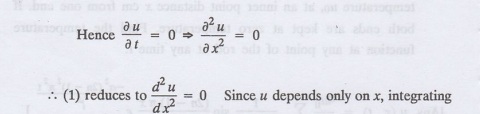
w.r.to x twice, we get the general solution as are arbitrary.

Example 3.4.b(3): What is the basic difference between the solution of one dimensional wave equation and one dimensional heat equation?

Solution :

Example 3.4.b(4): Distinguish between steady and unsteady states in heat conduction problems.

Solution: In unsteady state, the temperature at any point of the body depends on the position of the point and also the time t. In steady state, the temperature at any point depends only on the position of the point and is independent of the time t.

Example 3.4.b(5): A rod 30 cm long has its ends A and B kept at 20° and 80° respectively until steady state conditions prevail. The temperature at each end is then suddenly reduced to 0° C and kept so. Find the resulting temperature function u (x, t) taking x = 0 at A. 

Example 3.4.b(6): An insulated rod of length / has its ends A and B kept at a celsius and b° celsius respectively until steady state conditions prevail. The temperature at each end is suddenly reduced to zero degree celsius and kept so. Find the resulting temperature at any point of the rod taking the end A as origin.

Solution: The temperature function u (x, t) is the solution of the one dimensional heat equation.

c. Steady state conditions and non-zero Boundary conditions

Problems based on Steady state conditions and non-zero Boundary conditions

Example 3.4.c(1): A rod of length / cm with insulated sides has its ends A and B kept at a° celsius and b° celsius respectivley until steady state conditions prevail. The temperature at A is then suddenly raised to c° celsius and that at B is lowered to d° celsius. Find the subsequent temperature distribution u (x, t).

Example 3.4.c(2): The ends A and B of a rod 30 cms long have their VI temperature kept at 20° C and the other at 80° C until steady state conditions prevail. The temperature of the end B is then suddenly reduced to 60° C and kept so while the end A is raised to 40° C. Find the temperature distribution in the rod after time t.

d. Thermally insulated ends

Problems based on Thermally insulated ends