Statement Of Fourier Integral Theorem

STATEMENT OF FOURIER INTEGRAL THEOREM

Fourier integral theorem (without proof)

If f(x) is piece-wise continuously differentiable and absolutely integrable in (-∞, ∞), then

This is known as Fourier integral theorem or Fourier integral formula.

 (OR)

Let us assume the following conditions on a function f(x) sups

1. f(x) is piece-wise continuous in any finite interval (a,b)

2.  dx is convergent.

Then the Fourier integral theorem states that

The double integral in the right hand side is known as a Fourier integral expansion of f (x)

(OR)

If f(x) is a function defined in (-1, 1) satisfying Dirichlet's conditions, then

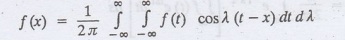
The double integral in the right hand side is known as Fourier integral to represent f (x)

Note: We assume the following conditions on f (x)

(i) f(x) is defined as single-valued except at finite points in (-1, 1)

(ii) f(x) is periodic outside (-1, 1) with period 2l

(iii) f(x) and f'(x) are sectionally continuous in (-1, 1)

 (iv) 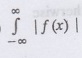  | f (x) | dx converges

i.e., f (x) is absolutely integrable in (-∞, ∞)

I.(a) Problems based on Fourier integral theorem :

Example 4.1.a(1): Show that f(x) = 1, 0 < x < ∞ cannot be represented by a Fourier integral.

Example 4.1.a(2):

Aliter:

Example 4.1.a(5) Find the Fourier integral of the function

4.1.b Complex form of the Fourier intergrals