Solved Example Problems based on Type 2 Clairaut's form z = = px + qy + f (p, q)

Problems based on Type 2.

TYPE 2. Clairaut's form z = = px + qy + f (p, q)

Example 1.3b(6): Solve z = px + qy + pq and classify the following integrals (i) z = ax + by + ab; (ii) z = 2x + 3y+6 (iii) z + xy = 0

Solution: Given: z = px + qy + pq

This equation is of the form z = px + qy + f (p,q)

Therefore, the complete integral is z = ax + by + f (a, b)

i.e., z= ax + by + ab 

To find the singular integral

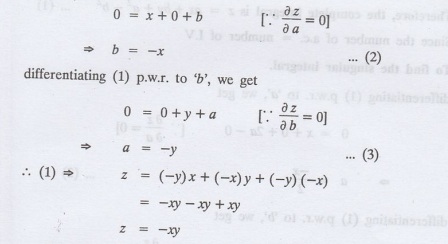
i.e., z + xy = 0 ... (4) which is the singular integral.

To get the general integral,

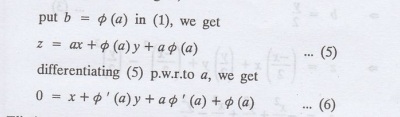
Eliminating 'a' between (5) & (6), we get the general solution.

Classification of integrals

(i) z = ax + by + ab + ab is a complete 1

(ii) z = 2x + 3y+6 is a particular integral. Since, Here a = 2, b = 3

(iii) z + xy = 0 is a singular integral.

Example 1.3b(7) : Solve z = px + qy + p² − q2.

[AU, April 2001] [A.U. N/D 2003, A/M 2008, M/J 2006] [A.U Tvli N/D 2010, Trichy N/D 2010] [A.U N/D 2014, R-13]

Solution: Given: z = px + qy + p² - q²

This equation is of the form z = px + qy + f (p,q)

[Clairaut's type]

Therefore, the complete integral is z = ax + by + a² - b²

Since the number of a.c. = number of I.V

 

To find the singular integral.

differentiating (1) p.w.r. to 'a', we get

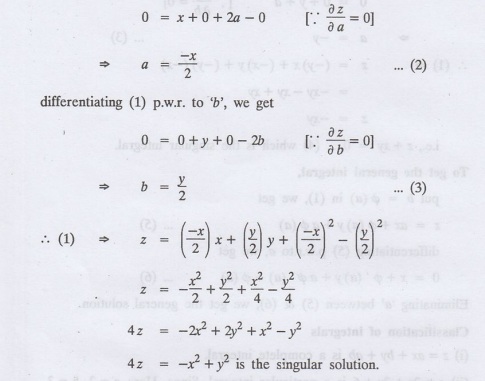
To get the general integral.

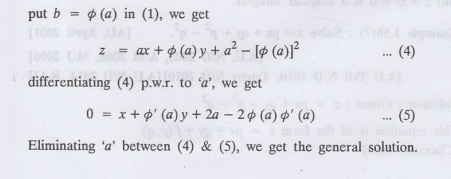
Example 1.3b(8) Find the complete integral of (pq) (z-px- qy) = 1.

Solution: Given: (p − q) (z - px - qy) = 1

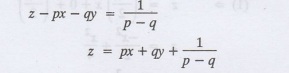
This equation is of the form z = px + qy + f (p,q) [Clairaut's equation]

Therefore, the complete integral is

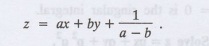
Since, the number of a.c. = number of I.V

Example 1.3b(9) Find the singular integral of z = px + qy + p²

Solution: Given: z = px + qy + p²

This equation is of the form z = px + qy +f(p,q)

[Clairaut’s type]

Therefore, the complete integral is z = ax + by + a2

Since the number of a.c = number of I.V

Example 1.3b(10): Solve z = px + qy + p² q²

Solution: Given: z = px + qy + p2 q²

eliminate 'a' between (6) & (7), we get the general solution.

Example 1.3b(11): Solve z = px + qy + √1+q² + ^p2.

Solution: Given: z = px + qy + √1+q²+p²

This is of the form z = px + qy + f (p,q)

[Clairaut's form]

Hence, the complete integral is z = ax + by + √1+ a² + ^b2 ... (1)  ́  where a and b are arbitrary constants.

 Since the number of a.c. = number of I.V

 Example 1.3.b(12) : Solve z = px + qy + √1 - p² - q²

Solution: Given: z = px + qy + √ 1 − ^p2 − q²

This is of the form z = px + qy + f (p,q) [Clairaut's form]

Hence, the complete integral is z = ax + by +√1-a²-b²

where a and b are arbitrary constants.

To get the singular integral :

Example 1.3b(13) : Obtain the complete solution of the equation px + qy - 2√pq

Solution: Given: z = px + qy - 2√pq

This is of the form z = px + qy + f (p,q) [Clairaut's form]

Hence, the complete solution is

z = ax + by - 2 √ab where a and b are arbitrary constants.

Since, the number of a.c. = number of I.V

Example 1.3b(14): Solve z = px + qy + (pq)^3/2.

Example 1.3b(15) Find the singular integral of z= Px + qy +p² + q²

Solution:

z= Px + qy +p² + q²

This equation is of the form z = px + qy + f (p,q) [Clairaut's type]

Therefore, the complete integral is z = ax + by + a² + b²

Since, the number of a.c. = number of I.V

To get the singular integral differentiating (1) p.w.r.to 'a' & 'b' we get

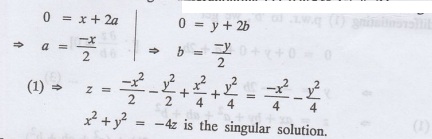
Example 1.3b(16) : : Find the complete integral of the partial differential equation  (1-x) p + (2-y)q = 3-z

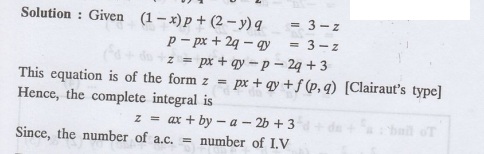
Example 1.3b(17): Find the singular integral of z = px + qy + p² + pq + q²

Solution : Given: z = px + qy + p² + pq + q²

This equation is of the Clairaut's form.

Hence, the complete solution is

z = ax + by + a² + ab + b²

Since, the number of a.c. = number of I.V

To find the singular integral.

Example 1.3b(18): Solve the equation

(pq-p-q) (z - px - qy) = pq

Solution:  Rewriting the given equation as

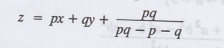
This is of the form z = px + qy + f (p, q) [Clairaut's form]

Hence, the complete solution is

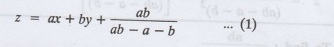
Since, the number of a.c. = number of I.V

To find the singular solution of (1).