Transforms And Partial Differential Equations: UNIT I: Partial Differential Equations
Solved Example Problems based on p.d.e Type 4 Separable equations
Partial Differential Equations
Transforms And Partial Differential Equations: UNIT I: Partial Differential Equations: Examples
Problems based on Type 4. Separable
equations.
Example
1.3b(31) : Solve p2y (1 + x2) = q2.
Solution:
Given: p2y (1+x2) = qx2

This is the complete integral where
a and b are arbitrary constants.
Differentiating partially w.r.to b,
we find that there is no singular integral.
Example
1.3b(32): Find the complete solution of p+q=sin x + sin y.
Solution:
Given: p + q = sin x + sin y
The given differentiating equation
can be written as
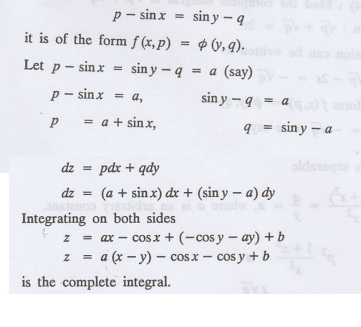
[We can solve this easily by
Lagrange's idea]
Example
1.3b(33): Find the complete integral of pq = xy.

Example
1.3b(34) Find the complete integral of Vp + √q = 2x.

Example
1.3b(35) Find the complete integral of p-1 x+q -1y = 1.
Solution
: Given: p-1 x+q -1y = 1.
The given equation can be written
as
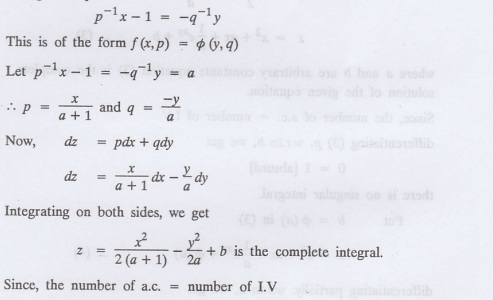
Example
1.3b(36): Solve the equation yp=2yx + log q.
Solution:

where a and b are arbitrary
constants equation (3) is the complete solution of the given equation.
Since, the number of a.c. = number
of I.V
differentiating (3) p. w.r.to b, we
get

Eliminate 'a' between (4) and (5),
we get the general solution.
Transforms And Partial Differential Equations: UNIT I: Partial Differential Equations : Tag: : Partial Differential Equations - Solved Example Problems based on p.d.e Type 4 Separable equations
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
