Transforms And Partial Differential Equations: UNIT III: Application Of Partial Differential Equations
Solutions Of One Dimensional Wave Equation
Examples
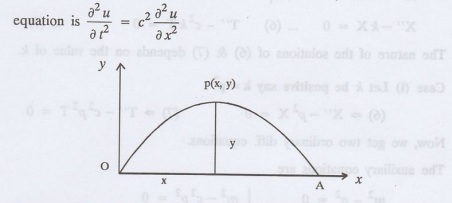
One dimensional wave equation: Consider an elastic string tightly stretched between two points O and A. Let O be the origin and OA as x-axis. On giving a small displacement to the string,
SOLUTIONS OF ONE DIMENSIONAL WAVE EQUATION
Equation
of a vibrating string :- One dimensional wave equation:
Consider an elastic string tightly stretched between two points O and A. Let O
be the origin and OA as x-axis. On giving a small displacement to the string,
perpendicular to its length (parallel to the y-axis). Let y be the displacement
at the point P (x, y) at any time. The wave
Example
3.3.1: Obtain the solution of one dimensional wave equation:
 p
p
Out of the three mathematically
possible solutions derived, we have to choose the solution which is consistent
with the physical nature of the problem and the given boundary conditions. In
the case of vibration of an elastic string, y (x, t) representing the
displacement of the string at any point x, y must be periodic in t. Hence
solution (9), which consists of periodic functions in t is the suitable solution
of the problems on vibration of strings. The arbitrary constants in the
suitable solution are found out by using the boundary conditions of the
problem. In problems, we directly assume that (9) is the suitable solution of
vibration of string problems.
The suitable solution (9) which is
periodic in 't is periodic in 'x' also.
Example
3.3.2: Derive D' Alembert's solution of the wave equation:

This solution is called D' Alemberts
solution of the one dimensional wave equation.
Example
3.3.3: State the assumptions made in the derivation of one dimensional wave
equation.
Solution:
The wave equation 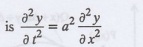
This gives y (x, t), the transverse
vibration of a string stretched to a constant tension T. In deriving this
equation, we make the following assumptions.
1. The motion takes place entirely
in one plane i.e., xy plane.
2. We consider only transverse
vibrations, the horizontal displacement of the particles of the string is
negligible.
3. The tension T is constant at all
times and at all points of the deflected string.
4. T is considered to be so large
compared with the weight of the string and hence the force of gravity is
negligible. 租
5. The effect of friction is
negligible.
6. The string is perfectly
flexible, i.e., it can transmit tension but not bus bending or shearing forces.
7. The slope of the deflection
curve at all points and at all instants is so small that sin a can be replaced
by a, where a is the inclination of the tangent to the deflection curve.
Example
3.3.4: Derive one dimensional wave equation :
Solution
:
Consider a tightly stretched elastic string of length with its end points
fixed. Let the string be released from rest and allowed to vibrate. The problem
is to determine the deflectior y (x, t) at any point x and at any time t >
0.
For deriving the p.d.e. we make the
following assumption.
See Example 3.3.3.
To
obtain the differential equation
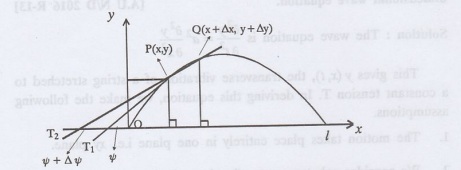
Take one end of the string as
origin O and take X-axis along the string.
We assume that the motion takes
place entirely in the XY plane. Consider the forces acting on a small portion
PQ of the string where P is (x, y) and Q is (x + ∆x, y + ∆y)
By assumption, the string does not
offer resistance to bending and shearing hence the tension at each point of the
string is tangential to the curve of the string.
Jon Let T1 and T2
be the tensions at the points P and Q.
Letφ and φ + ∆φ be the angles made
by the tangents at P and Q respectively with the X axis.
Let m be the mass per unit length
of the string
Since, there is no motion in the
horizontal portion of the string ast od lo noitsailoni the tension must be
constant.
.. T1 cos φ = T2 cos (φ+
∆φ) which is a constant.
Sinceφ is small, cosy φand cos (φ+∆φ)
are approximately equal to 1.
Thus, T1 = T2
= T, a constant.
The vertical component of the force
acting on the element PQ is
T sin (φ+∆φ) - T sinφ= T (φ + ∆ φ)
− Tφ
['. sin φ = φwhereφ is small]
The acceleration of the element in
the y direction is ![]()
Hence, by Newton's second law of
motion,
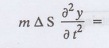 = T ∆φ where m is the mass per unit length of
the string.
= T ∆φ where m is the mass per unit length of
the string.
as ∆S is the length of the element
PQ.
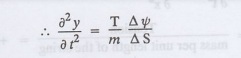
Taking limit as as ∆S→ 0, we get

This partial differential equation
is known as the one dimensional wave equation. It is a homogeneous of second
order.

Problem
on vibrating string with zero initial velocity.
Type
1. Vibrating string with zero initial velocity:
The boundary and initial conditions
of the deflection y (x, t) are

The suitable solution is
(x,t) = (c1 cos px + c2 sin
px) (c3 cos p at + c4 sin p at)
Apply condition (i), we get c1
= 0
Apply condition (ii), we get 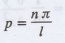
Apply condition (iii), we get c4
= 0
The most general solution is
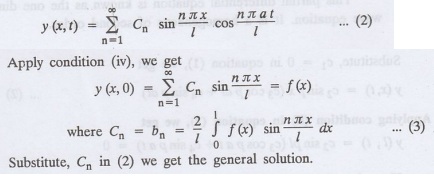
Example
3.3.6 : A string is stretched and fastened to two points x = 0 and x = 1 apart.
Motion is started by displacing the string into the form y = k (lx - x) from
which it is released at time t = 0. Find the displacement of any point on the
string at a distance of x from one end at time t.
Solution:
The wave equation is 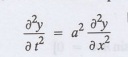
From the given problem, we get the
following boundary & initial conditions.

Now, the suitable solution which
satisfies our boundary conditions is given by

Applying
condition (i) in equation (1), we get
y (0,t) = (c1+0) (c3
cos p at + c4 sin p at)……………………....(1)

Substitute, c1 = 0 in
equation (1), we get (vi) noilib
y (x, t) C2 sin px (c3
cos p at + c4 sin p at)
Applying
condition (ii) in equation (2), we get
y (l, t) = c2 sin pl (c3
cos p at + c4 sin pat) = 0
Here, [c3 cos pat + c4
sin pat] 0 [. it is defined for all t]
Therefore, either c2 bart 0 =0

Example
3.3.7: Find the displacement of a string of length '7' vibrating between fixed
end points with initial velocity zero and initial displacement is given by

Example
3.3.8 : A string of length 21 is fastened at both ends. The mid point of the
string is taken to a height b and then released from rest in that position.
Show that the displacement is

Example
3.3.9 : A tightly stretched string of length has its ends fastened at x = 0 and
x = 1. The mid point of the string is then taken to a height hand then released
from rest in that position. Obtain an expression for the displacement of the
string at any subsequent time.

Example
3.3.10 : The points of trisection of a string of length / with fixed ends aside
through a distance h on opposite sides of the position of equilibrium and the
string is released from rest. Find an expression for the displacement of the
string at any subsequent time. Also show that the mid point of the string
always remains at rest.
Solution:
Taking the end points as origin O and A on the x axis, the initial position of
the string is given in the figure.

Example
3.3.11: If a string of length /is released from rest in the position
ppppppppppppp show that the motion is
described by the equation.

Example
3.3.12: A tightly stretched string with fixed end points x=0 and x = /
initially displaced in a sinusoidal arc of length yo and then released from
rest. Find the displacement y at any distance x from one end at time t.

Example 3.3.13 : An elastic string is stretched between two points at a distance л apart. In its equilibrium position the string is in the shape of the curve f (x) = k (sin x – sin3 x). Obtain y(x, t) the vertical

Example
3.3.14: A string of length l has its ends x = 0, x = l fixed. The point where x
= l/3 is drawn aside a small distance h, the displacement y (x, t) satisfies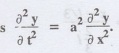 Find y(x, t) at any time t.
Find y(x, t) at any time t.

Transforms And Partial Differential Equations: UNIT III: Application Of Partial Differential Equations : Tag: : Examples - Solutions Of One Dimensional Wave Equation