Transforms And Partial Differential Equations: UNIT II: Fourier Series
Questions And Answers
Transforms And Partial Differential Equations: UNIT II: Fourier Series: Questions And Answers
PART-A QUESTIONS AND ANSWERS
I.
Problems under (0, 2), (0, 2), (-л, л), (−1, 1)
1.
When does a function possess a Fourier series expansion in terms of
trignometric terms?
(or) State the conditions for f(x) to have Fourier
series expansion.
(or) Explain Dirichlet's
conditions.
Solution :
2.
State whether y = tan x can be expanded as a Fourier series. If so how? If not
why ?
Solution:
tanx cannot be expanded as a Fourier series. Since, tanx does not satisfy
Dirichlet's conditions.
[tanx has infinite number of
infinite discontinuities.]
3.
Find the sum of the Fourier series for

4. If the Fourier series for the functiones.
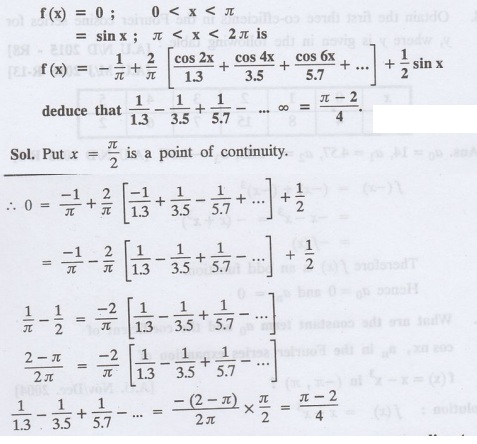
5. Find the constant term in the
Fourier series corresponding to

6.
Write ao, an in the expansion of x + x3 as a
Fourier series in (-л, π).
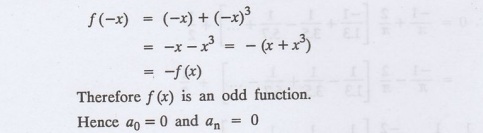
7.
What are the constant term ao and the coefficient of cos nx, an in
the Fourier series expansion of
f (x) = x − x3 in (−ñ, ñ) ?
Solution:
f(x)
= x-x3
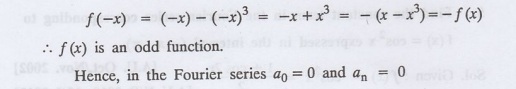
8.
In the Fourier expansion of

9.
If f(x) = x2 + x is expressed as a Fourier series in the interval
(-2, 2) to which value this series converges at x = 2?
Solution
:
x = 2 is a point of discontinuity in the extremum.
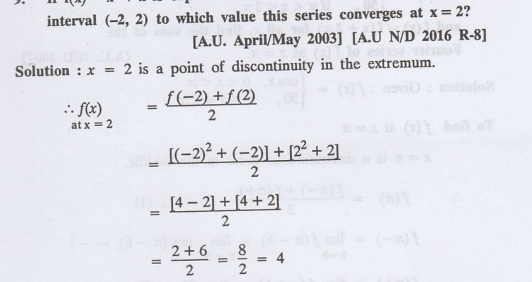
10.
Find b1 in the expansion of as a Fourier Series in (-л, л).
Solution
:
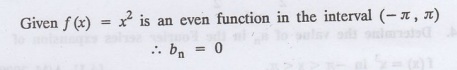
11.
If f(x) is an odd function defined in (-1, 1), what are the values of a0
and an
Solution:
Given f(x) is an odd function in the interval (-1, 1)
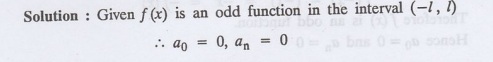
12.
Find the Fourier constants bn for x sin x in (-л, л).
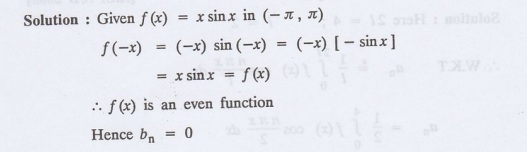
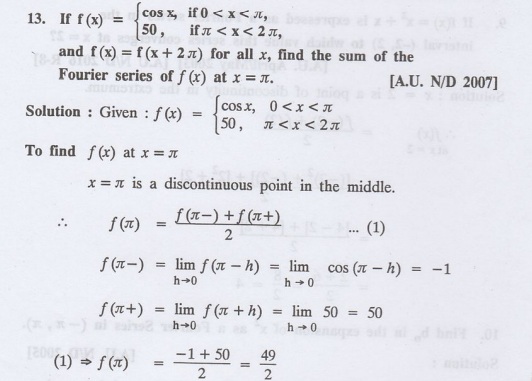
14.
Determine the value of an in the Fourier series expansion of f(x) =
x3 in −л < x <л.
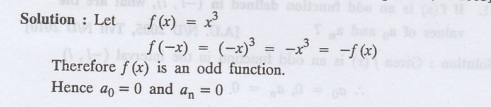
15.
If f (x) = 2x in the interval (0, 4), then find the value of a2in
the Fourier series expansion.
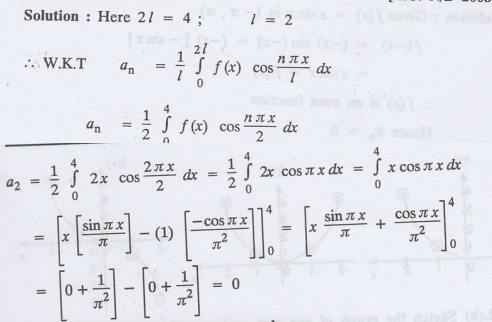
II. Problems under Half range series
1.
Find half range sine series for f (x) = k in 0 < x <л.
Solution:
The sine series of f (x) in (0, л) is given by
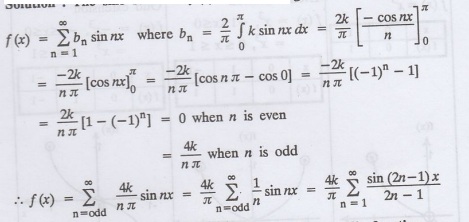
2.(a)
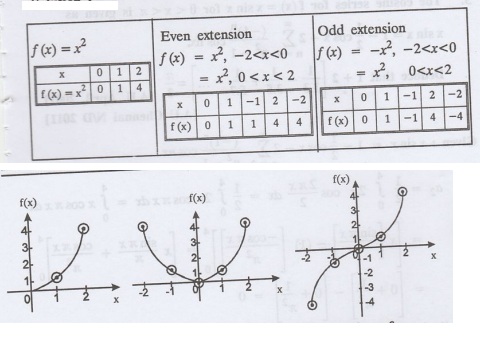
Sketch the even and odd extension of the periodic function
f(x)
= x2 for 0 < x <2
Solution
:
2.(b)
Sketch the graph of one even and one odd extension of ƒ (x) = x3 in
[0, 1]
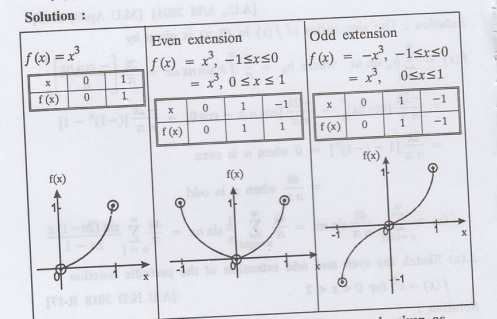
3.
The cosine series for f (x) = x sin x for 0 < x <л is given as

4. Expand f(x) = 1 in a sine series in 0 < x < л.
Solution:
The sine series of f (x) in (0, л) is given by
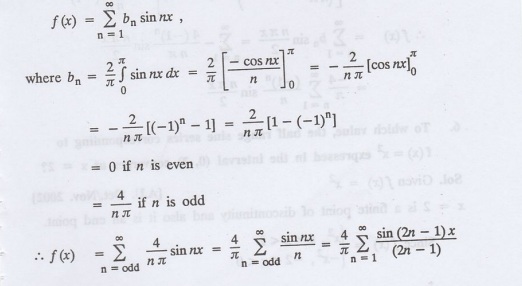
5.
Find the Fourier sine series of f (x) = x in 0 < x < 2.
Solution:
In the interval 0 < x < 2 the half range sine series for
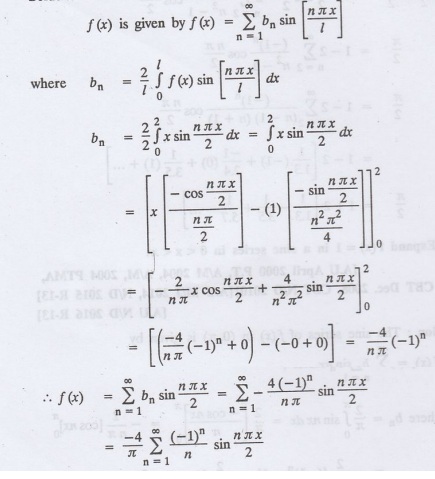
6.
To which value, the half range sine series corresponding to f(x) = x2
expressed in the interval (0, 2) converges at x = 2?
Sol.
Given f(x)
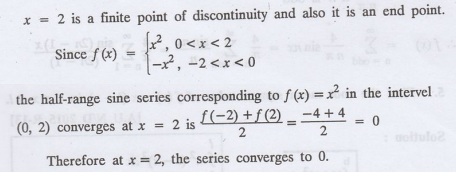
III. Problems under Parseval's identity, R.M.S value
1.
State Parseval's identity for the half-range cosine expansion of f(x) in (0,
1).
Solution: 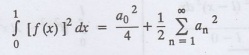
2 Find the root mean square value
of the function f(x) = x in the interval (0, 1).
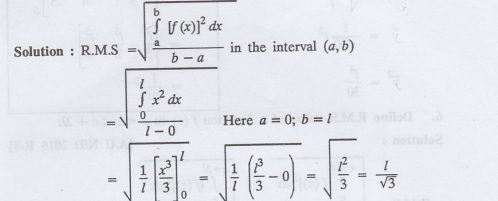
3.
Define root mean square value of a function f(x) in a < x < b.
Solution:
Let f (x) be a function defined in an interval (a, b) then

4.
What do you mean by Harmonic Analysis?
Solution: The process of finding Euler constant for a tabular function is known as Harmonic Analysis.
5.
Find the root mean square value of f (x) = x (1-x) in 0 ≤ x ≤l.
Solution
:

6.
Define R.M.S value of a function f (x) in c <x<c + 21.
Solution
:
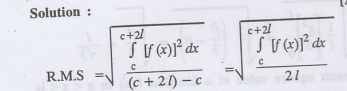
7.
State TRUE or FALSE : Fourier series of period 20 for the nod function f(x) = x
cos (x) in the interval (-10, 10) contains only sine terms. Justify your
answer.
Solution
:
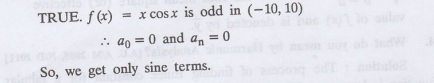
Transforms And Partial Differential Equations: UNIT II: Fourier Series : Tag: : - Questions And Answers
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
