Problems on vibrating string with non-zero initial velocity

Problems on vibrating string with non-zero initial velocity.

Type 2. Vibrating string with non-zero initial velocity :

Example 3.3.15: A tightly stretched string with fixed end points x=0 and x = 1 is initially at rest in its equilibrium position. If it is set vibrating string giving each point a velocity 2 x (1-x) show that the displacement is

Example 3.3.16: If a string of length a is initially at rest in its equilibrium position and each of its points is given a velocity kx (a-x), determine the displacement function.

Solution In Example 3.3.15 Put = a and λ = k

Example 3.3.17 : A tightly stretched string with fixed end points x = 0 and x = L, is initially in its equilibrium position. If it is set vibrating giving each point a velocity 3x (L-x), find the displacement.

Solution: In Example 3.3.15

Here, Put / = L and 1 = 3

Example 3.3.18: A tightly stretched string with fixed end points x=0, and x = L is initially in a position given by y = Lx − & it is released from rest from this position, find the displacement y(x, t)

Solution: In Example 3.3.15

Here, put l = L and λ = 1

Example 3.3.19: If a string of length is initially at rest in its equilibrium position and each of its points is given the velocity 3 πχ/l  0 < x < 1, determine the displacement of a point distant x from one end at time 't'.

Example 3.3.20: A string of length / is initially at rest in its equilibrium position and motion is started by giving each of its points a velocity

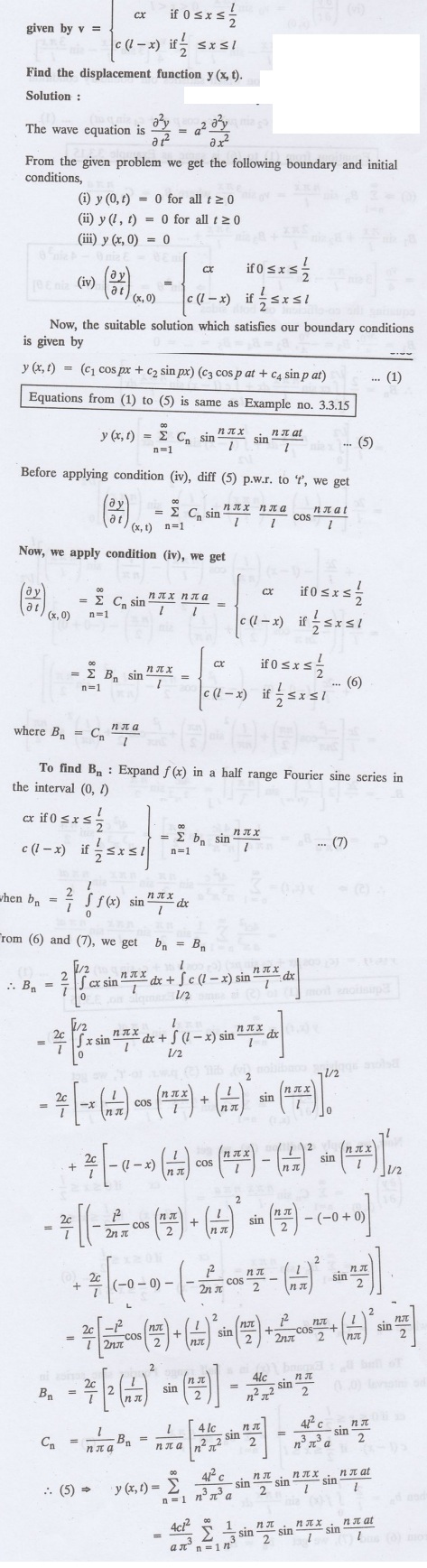
Example 3.3.21: If the string of length / is initially at rest in equilibrium position and each of its points is given the velocity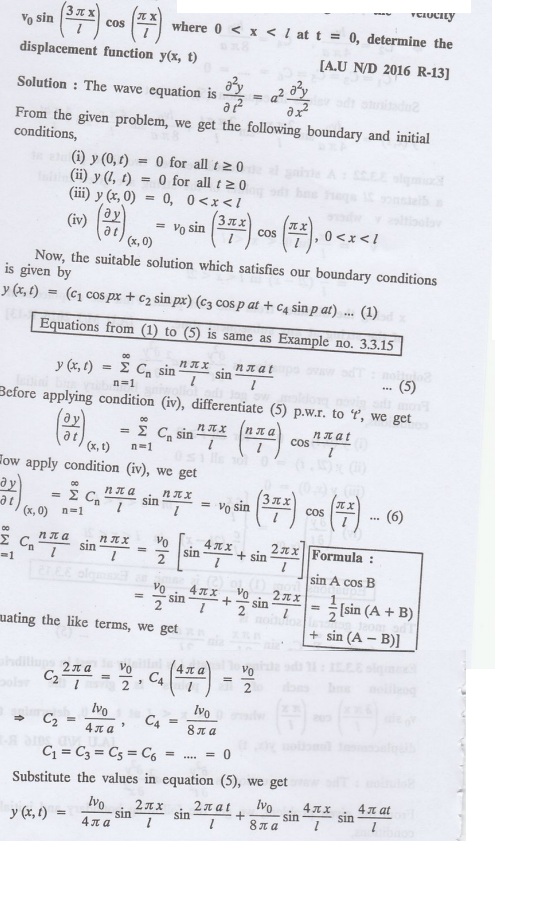 

Example 3.3.22: A string is stretched between two fixed points at a distance 21 apart and the points of the string are given initial velocities v where