Problems based on formation of p.d.e by elimination of arbitrary constants (a.c.)

I. Problems based on formation of p.d.e by elimination of leno arbitrary constants (a.c.)

Example 1.1a(1): Form the p.d.e. by eliminating the arbitrary constants a & b from z = ax + by.

Solution: Given: z = ax + by…………….(1) 

differentiating (1) partially w.r. to 'x', we 

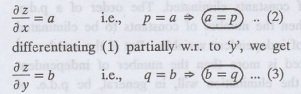
Substituting (2) & (3) in (1), we get the required p.d.e z = px + qy.

Example 1.1a(2) : Eliminate the arbitrary constants a & b from z = ax + by + a² + b²

.

Solution: Given: z = ax + by + a² + b²

differentiating (1) partially w.r. to 'x', we get

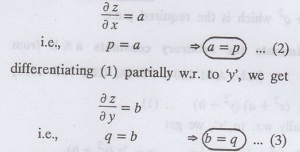
.. Substituting (2) & (3) in (1), we get the required p.d.e

z = px + qy + p² + q²

Example 1.1a(3): Form the p.d.e by eliminating the arbitrary constants from z = ax + by + ab

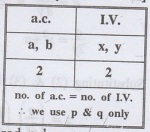
Solution: Given: z = ax + by + ab......(1)

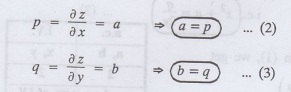
Substituting (2) & (3) in (1), we get the required p.d.e.

i.e., z = px + qy + pq

Example 1.1a(4) : Form a p.d.e by eliminating the arbitrary constants a and b from z = (x + a)² + (y - b)²

Solution: Given: z = (x + a)² + (v - b)^{2.............(1)}

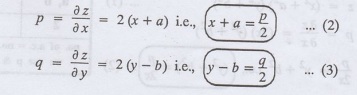
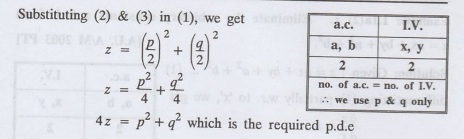
Example 1.1a(5): Eliminate the arbitrary constants a &b from z=(x²+a) (y²+b)

Solution: Given: z = (x² + a) (v² + b) ……………....(1)

differentiating (1) partially w.r. to 'x', we get

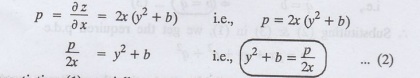
differentiating (1) partially w.r. to 'y', we get

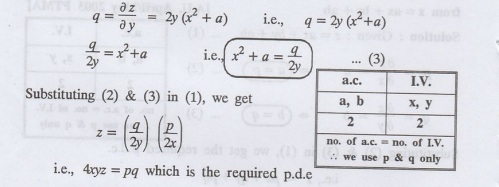
Example 1.1a(6): Form the partial differential equation by eliminating a and b from z = (x² + a²) (y²+ b²)

Solution: Given :

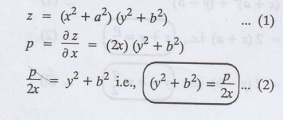
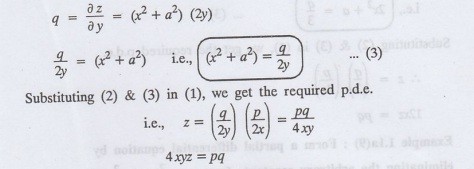
Example 1.1a(7): Form the p.d.e. by eliminating the constants a and b from z=axⁿ +byⁿ

Solution:

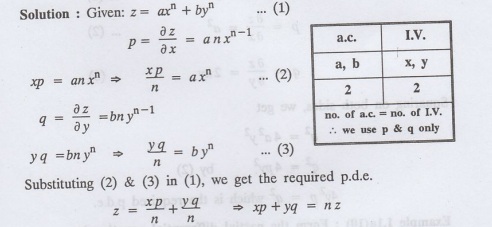
Example 1.1a(8): Form a partial differential equation by eliminating the arbitrary constants a and b from the relation

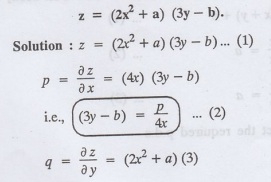
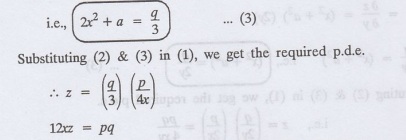
Example 1.1a(9) Form a partial differential equation by eliminating the arbitrary constants from z = a²x + ay² + b

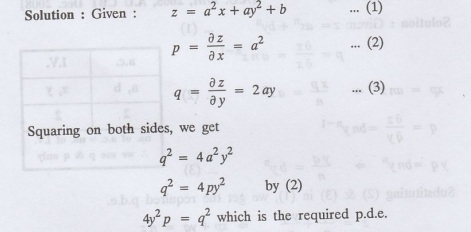
Example 1.1a(10) : Form partial differential equation by eliminating  a and b from  z = a (x + y) + b

Solution:

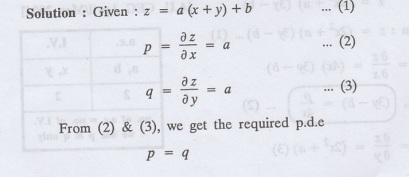
Example 1.1(a) (11) : Form the p.d.e. by eliminating the arbitrary constants a & b from z = axe^y + 1/2  a² e^2y + b.

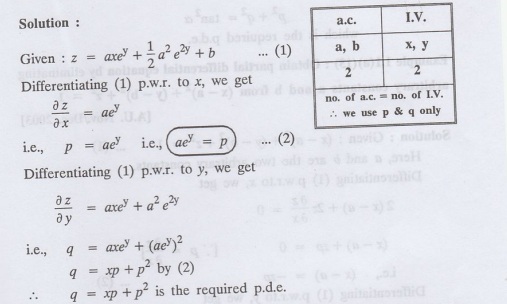
xample 1.1(a) (12) : Form the partial differential equation by eliminating a and b from (x − a)² + (y − b)² = z² cot² a

Solution: The given equation is

Example 1.1(a) (13): Obtain partial differential equation by eliminating arbitrary constants a and b from (x − a)² + (y - b)² + z² = 1.

Example 1.1(a) (14) Find the p.d.e. of all planes through the origin.

Solution: The general equation to a plane is = ax+by+cz+d  =0 ... (1)

Example 1.1(a)(15) : Find the p.d.e of all sphere whose centres lie on the z axis.

Solution: Let the centre of the sphere be (0, 0, c) a point on the z axis and k its radius (arbitrary)

Example 1.1(a)(16): Find the p.d.e. of all spheres of radius 'c' having their centres in the XOY plane.

Solution: Let the centre of the sphere be (a, b, 0) a point in the XOY plane, 'c' is the given radius.

The equation to the sphere is

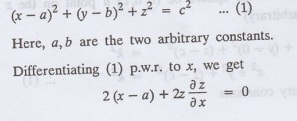
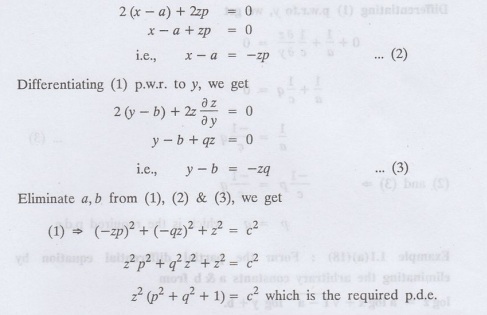
Example 1.1(a) (17) Find the PDE of all planes having equal intercepts on the x and y axis.

Example 1.1(a) (18) : Form the partial differential equation by eliminating the arbitrary constants a & b from

log z = a log x + √1 – a² log y + b.

Solution:

Example 1.1(a)(19): Form the partial differential equation by 

Example 1.1(a) (20) Form the p.d.e. by eliminating the arbitrary constants a & b from

Example 1.1(a)(21): Find the partial differential equation of the family of spheres having their centres on the line x = y = z.