Methods to solve the first order partial differential equation

(2) Methods to solve the first order partial differential equation.

The general form of a first order partial differential equation is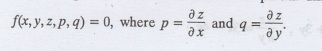 

§ Mention three types of solution of a p.d.e. (or) Define P.I, general and complete integrals of a p.d.e.

1. Complete integral (or) Complete solution

A solution which contains as many arbitrary constants as there are independent variables is called a complete integral (or) complete solution. (number of a.c. = number of I.V)

2. Particular integral (or) Particular solution

A solution obtained by giving particular values to the arbitrary constants in a complete integral is called a particular integral (or) particular solution.

3. General integral (or) General solution

A solution of a p.d.e. which contains the maximum possible number of arbitrary functions is called a general integral (or) general solution.

Example (i): z = ax + by + ab

Number of a.c = Number of I.V

Hence, z = ax + by + ab is a complete integral.

Example (ii) : z = 2x + 3y+6 is a particular integral.

Since, a = 2, b = 3 are the particular values of the complete integral z = ax + by + ab

Example (iii) :

z = ƒ (x² − y²) ... (1) is the solution of p.d.e

yp + xq = 0... (2)

Here, yp +xq = 0 is a p.d.e of order 1.

So, the maximum possible number of a.f. = 1

z = f(x2 - y2) is a general solution of (2).

§ Show how to find the general integral of the p.d.e. f(x, y, z, p, q) = 0.

Solution :

Let the p.d.e be f(x,y,z,p,q) = 0 ……….(1)

Let the complete integral of (1) be p (x, y, z, a,b) = 0 ... (2)

where a & b are arbitrary constants.

Suppose, in (2) one of the constants is a function of the other say b = f(a). Then (2) becomes

Differentiating (3) p.w.r. to a we get

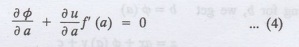
The elimination of 'a' between (3) & (4) if it exists, called the general integral of (1).

§ Define singular integral.

Solution: Let f (x, y, z,p,q) = 0……………(1)

Let the complete integral be (x, y, z,a,b)………………..(2)

Differentiating (2) p.w.r. to a and b in turn we get,

The elimination of a & b from the three equations (2), (3) & (4) if it exists, is called the singular integral.

Type 1 f(p, q) = 0

Suppose that z = ax + by + c

Then p = a, q=b

we get, f (a, b) = 0

solving for b, we get b = ϕ(a)

z= ax + ϕ(a)y + c ………………(1)

which is the required complete integral.

Differentiating (1) p. w.r.to c, we get 0 = 1 which is absurd that there is no singular integral.

Put cf (a) in (1) we get

z = ax + (a) y + f (a)………………(2)

Differentiating (2) p. w.r.to a we get

0 = x + ᴓ (a)y + f (a) ……(3)

eliminating 'a' between (2) and (3), we get the general solution.