Harmonic Analysis

HARMONIC ANALYSIS

Sometimes the function is not given by a formula, but by a graph or by a table of corresponding values. The process of finding the Fourier series for a tabular form of numerical values is known as Harmonic Analysis. The Fourier constants are evaluated by the following formulae :

Fundamental or first harmonic. The term (a cosx+b1 sinx) in Fourier series is called the fundamental or first harmonic.

Second harmonic: The term (a2 cos 2x + b2 sin 2x) in Fourier series is called the second harmonic and so on.

Note: 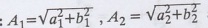 are the amplitudes of the first will decrease rapidly. and second harmonic. The amplitudes A₁, A2, Hence, the first few harmonics give a good result to the given function.

Type 1 Given data are in л form

Type 2: Given data are in degree form

Type 3 Given data are in T form

Type 4: Given data are in / form 

Problems based on Harmonic Analysis

TYPE 1: GIVEN DATA ARE IN FORM

Example 2.6.1 : Find the Fourier Series upto the third harmonic for y = f(x) in (0, 2) defined by the table of values given below. 

Example 2.6.2: Determine the first two harmonic of the Fourier series for the following values.

TYPE 2 GIVEN DATA ARE IN DEGREE FORM

Example 2.6.3: Find an empirical formula of the form

f(x) = a_o + a₁ cos x + b₁ sin x

for the following data given that f(x) is periodic with period 2 л.

Example 2.6.4: Compute the first three harmonies of Fourier series of f(x) given by the following data.

TYPE 3 GIVEN DATA ARE IN T FORM

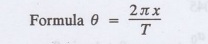
Example 2.6.5: The values of x and the corresponding values of f(x) over a period T are given below, Show that

TYPE 4. GIVEN DATA ARE IN  l FORM

Example 2.6.6: Find the first two harmonics of the Fourier series from the following table.