Half-Range Series

HALF-RANGE SERIES

(a) HALF-RANGE SINE SERIES

(b) HALF-RANGE COSINE SERIES

Sine series: To expand f(x) as a sine series in (0,л) or (0,1), we extend the function reflecting it in the origin, so that f(x) = f (x).

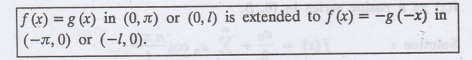
Cosine series: To expand f(x) as a cosine series in (0,л) or (0,1), we extend the function reflecting it in the y-axis, so that f(x) = f(x).

Example 2.3.1: Write the formula for formula for Fourier constants to expand f(x) as a sine series in (0, л).

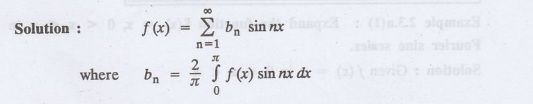
Example 2.3.2: Write the formula for Fourier constants to expand f(x) as a sine series in (0, l).

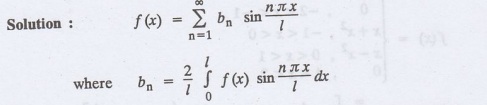
Example 2.3.3: Write the formula for Fourier constants to expand f(x) as a cosine series in (0, л).

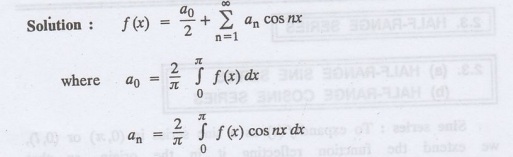
Example 2.3.4: Write the formula for Fourier constants to expand f(x) as a cosine series in (0, 1).

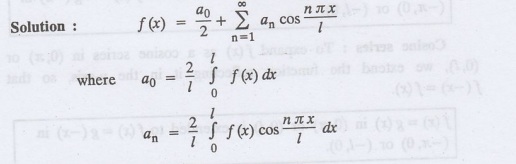
(a) HALF-RANGE SINE SERIES

Problems based on Half-Range Sine Series

Example 2.3.a(1): Expand the function f(x) = x, 0 < x < л in Fourier sine series.

Solution: Given f(x) = x in 0 < x < л

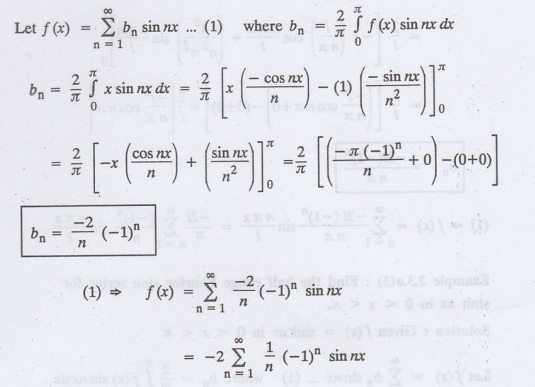
Example 2.3.a(2): Find the Half range Fourier sine series for (x) = = x in (0, 1).

Solution: Let the required Fourier series be

Example 2.3.a (3): Find the half range Fourier sine series for sinh ax in 0 < x < π.

Example 2.3.a(4): Find the half range sine series for the function f(x) = x - x², 0 < x < 1

Solution:

Example 2.3.a(5): Find the sine series of f(x) e^x in (0, π)

Solution: Let the required Fourier series be

Example 2.3.a(6): Find the Fourier sine series of f (x) = 1-x in (0, 1)

Example 2.3.a(7): Find the Half range sine series for f (x) = x ( − x) in (0, л). Deduce thatpppppppppppp

Solution: Let the half range sine series be

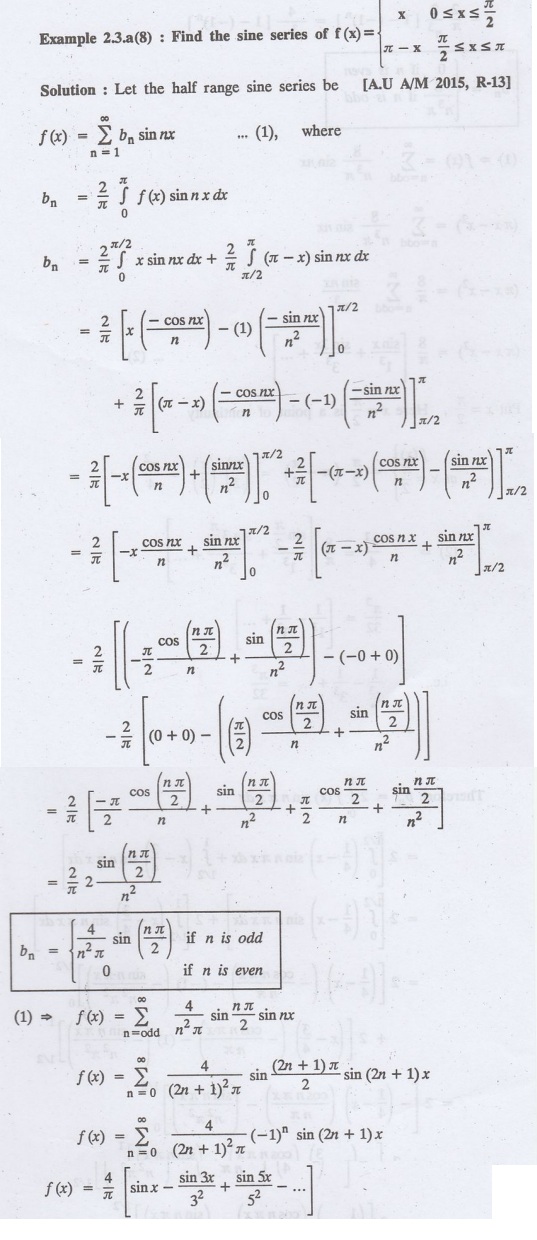
Example 2.3.a(9): Express f(x) as a Fourier sine series where

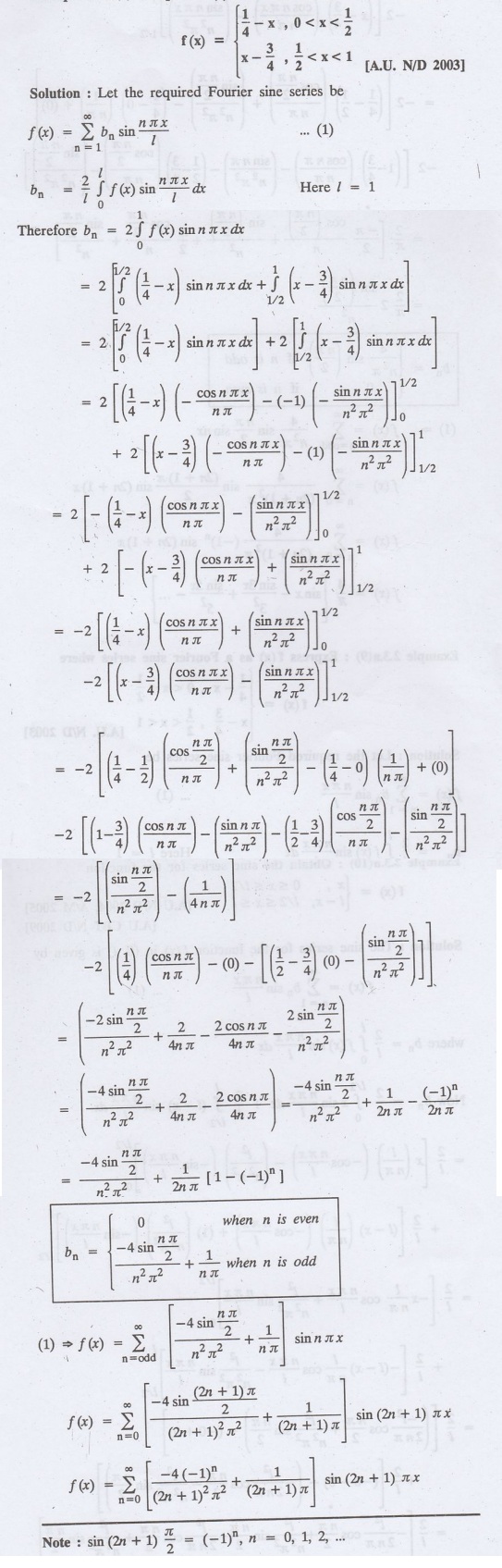
Example 2.3.a(10): Obtain the sine series for the function

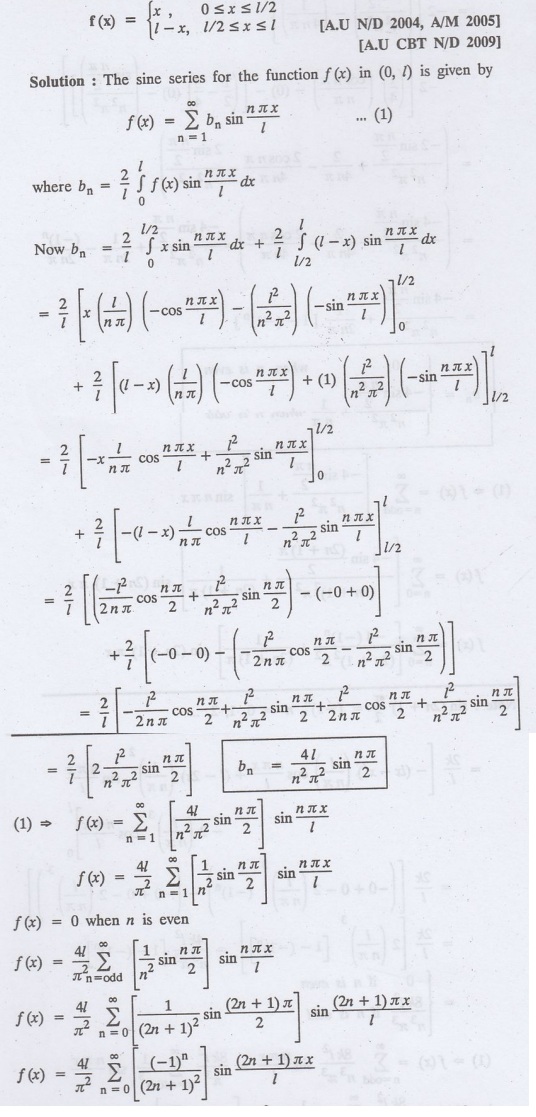
Example 2.3.a(11): If ƒ (x)=k (kx − ^x2) in the range (0, 1), show that the half range sine series for

(b) Half-rangecosine series

Problems based on Half-Rangen cosine series

Example 2.3.b(1): Find the Fourier cosine series for f(x) = x² <x<π

Example 2.3.b(2): Expand the function f(x) sin x, 0 < x <л in Fourier cosine series.

Solution: Let the required Fourier cosine series be

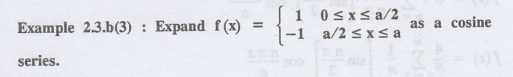
Example 2.3.b(4) Find the Half-range cosine series for  f(x) = 

Example 2.3.b(5): Find the cosine series of f (x) = e* in (0, 1). Solution: Let the required Fourier cosine series be

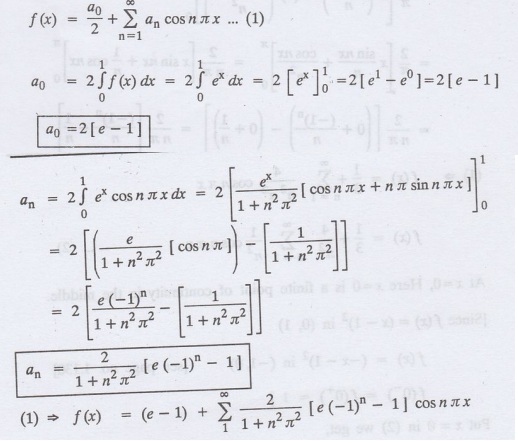
2.3.b(6) Find the half range cosine series of f (x) = x in 0<x< π.

Example 2.3.b(7): Find the half range cosine series of f (x) = (π − x²) in the interval (0,π).

Example 2.3.b(8): Find the half-range cosine series for the function f(x) = x  (лx) in 0 < x < л.