Fourier Sine & Cosine Transforms

FOURIER SINE & COSINE TRANSFORMS:

FOURIER COSINE TRANSFORM:

The infinite Fourier cosine transform of f (x) is defined by

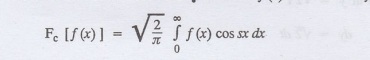
The inverse Fourier cosine transform Fc [f(x)] is defined by

 

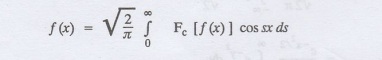
INVERSION FORMULA FOR FOURIER COSINE TRANSFORM

Let F_e(s) denote the F.C.T of f(x). Then

 

FOURIER SINE TRANSFORM:

The infinite Fourier sine transform of f(x) is defined by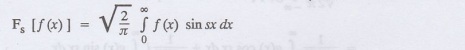 

The inverse Fourier sine transform of F, [f(x)] is defined by 

 

INVERSION FORMULA FOR FOURIER SINE TRANSFORM

 

Properties of Fourier sine transform and Fourier cosine transform

1. Linear property

2. Modulation property :

 

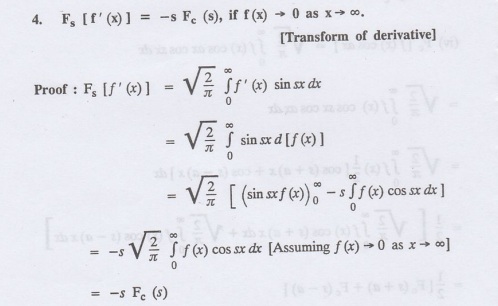
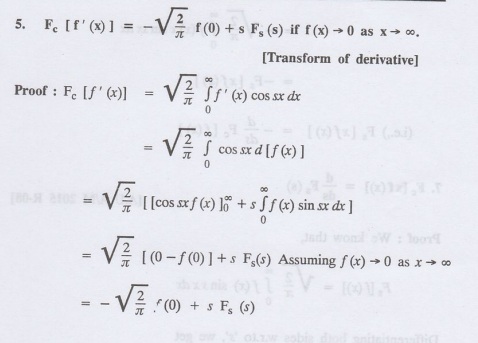
III (a). Problems based on Fourier Cosine Transform

Formula:

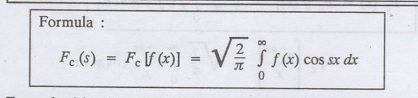
Example 4.3.a(1) Find the Fourier cosine transform of

 

 

Example 4.3.a(3): Find the Fourier cosine transform of e ^-ax a > 0.

Solution:

 

Example 4.3.a(4): Find the Fourier cosine transform of the function 3e ^-5x +5e^-2x

 

Example 4.3.a(5): Find the Fourier cosine transform of

Example 4.3.a(6):Find the Fourier cosine transform of f(x) = x.

Solution: We Know that,

Example 4.3.a(7):Find the Fourier cosine transform of e^-ax cosax.

Solution: We Know that,

Example 4.3.a(8): Show that e^x2/2 is self-reciprocal under Fourier cosine transform.

Solution :

We know that,

 

Example 4.3.a(9): Find the Fourier cosine transform of e^-ax  sin ax.

Solution: We know that,

Example 4.3.a(10): Evaluate Fe [x^n-1] if 0 < x < 1. Deduce that 1/x is self reciprocal under Fourier cosine transform.

Solution :

 

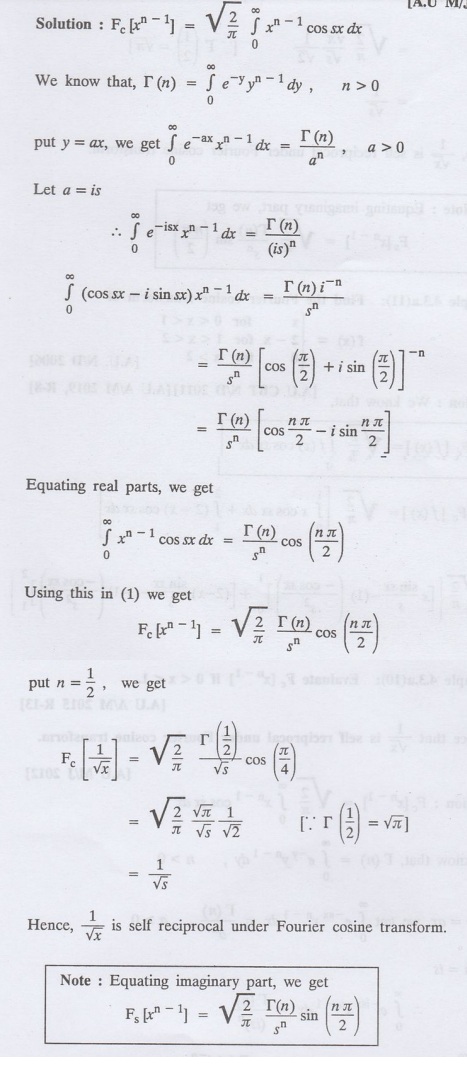
Example 4.3.a(11): Find the Fourier cosine transform of

 

 

Example 4.3.a(13): Find the Fourier cosine transform of e^{-a2x2 ̧}

Solution: We know that,

III. (b) Problems based on Fourier cosine transform and its inversion formula.

Formula :

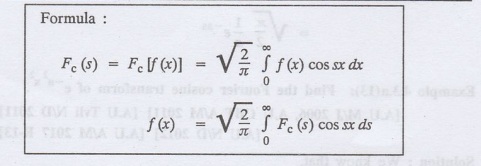
Example 4.3.b(1): Solve the integral equation

Example 4.3.b(2): Solve the integral equation

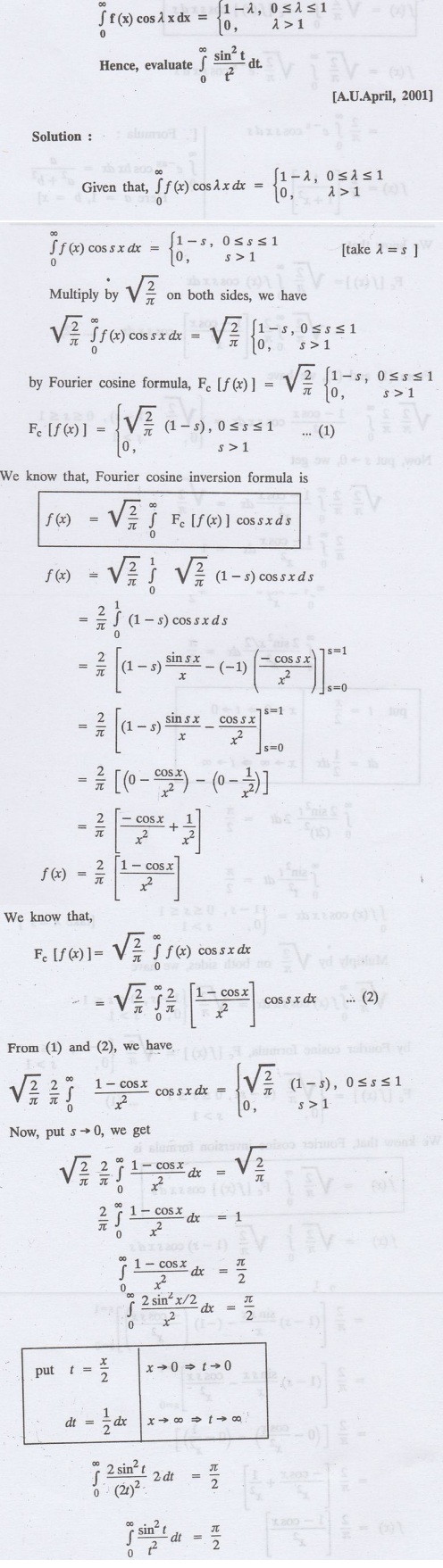
Example 4.3.b(3): Find the Fourier cosine transform of e^{- |x|} 

Example 4.3.b(4): Find the Fourier cosine transform of e^-ax, a 

 

III. (c) Problems Based on Fourier Sine Transform. [F.S.T]

Formula :

 

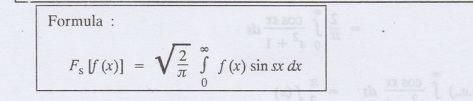
Example 4.3.c(1): Find the Fourier sine transform of

 

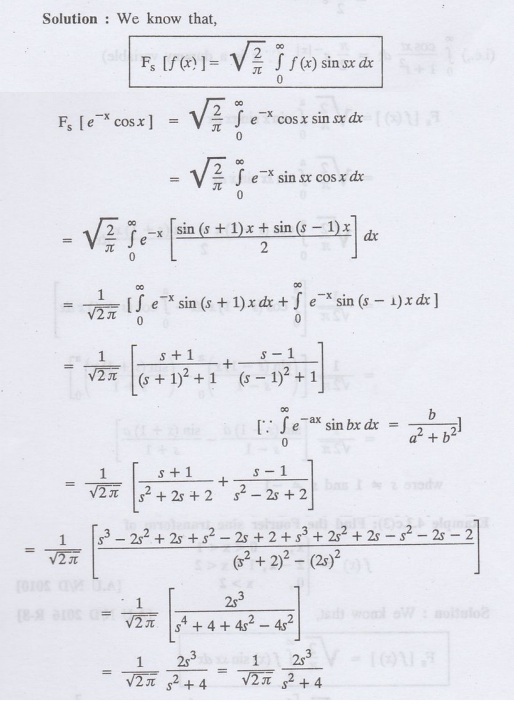
Example 4.3.c(2): Find the Fourier sine transform of

 

Example 4.3.c(3): Find the Fourier sine transform of

 

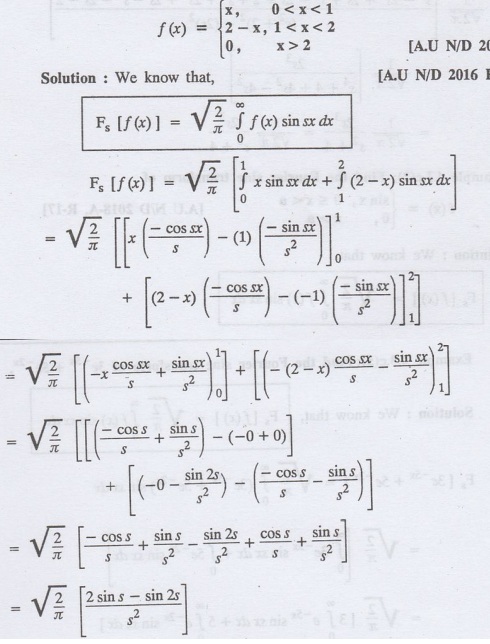
Example 4.3.c(4): Find the Fourier sine transform of 1/x

Solution: We know that,

 

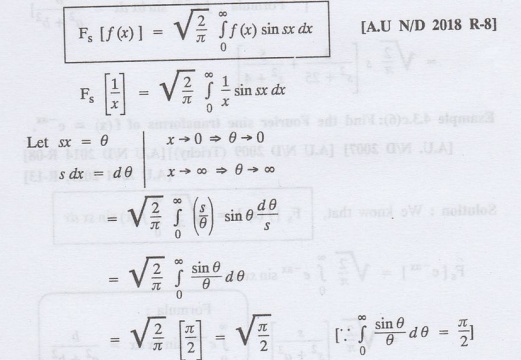
Example 4.3.c(5): Find the Fourier sine transform of 3e^-5x +5e^-2x

Solution: We know that,

 

Example 4.3.c(6): Find the Fourier sine transforms of f (x) = ^e-ax

Solution: We know that,

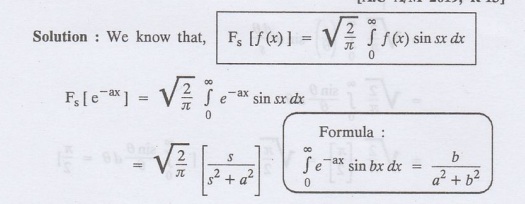
Example 4.3.c(7): Find the Fourier sine transform of the function

 

Example 4.3.c(8): Find the Fourier sine transform of ^{x n-1}. Deduce that is 1/√x self reciprocal under Fourier sine transform.

 

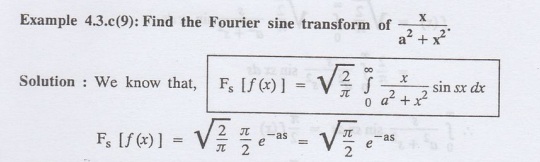
III. (d) Problems based on Fourier sine transform and its inversion formula.

Formula :

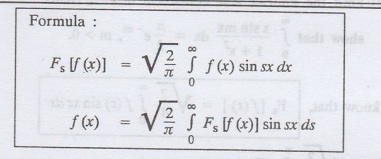
Example 4.3.d(1): Find Fourier sine transform of e^-ax a > 0 and 

 

Example 4.3.d(2): Find the Fourier sine transform of e^-x  Hence 

 

Example 4.3.d(4): Solve the integral equation

 

III .(e) Problems based on properties of F.C.T AND F.S.T.

Example 4.3.e(1): (i) Find the Fourier cosine transform of 

 

Example 4.3.e(2):  Find the Fourier sine and cosine transformations of  xe-^ax

Solution: (i) We know that,

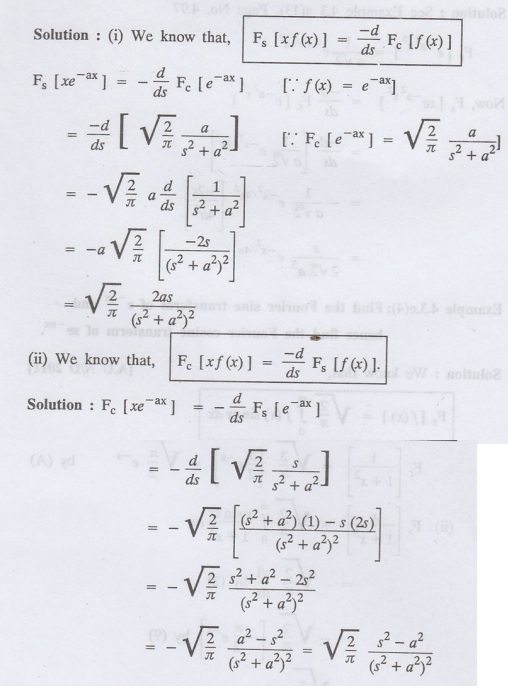
Example 4.3.e(3): Find Fourier cosine transform of e –a² x² 

Example 4.3.e(4): Find the Fourier sine transform of e^-ax hence find the Fourier cosine transform of xe^-ax 

Solution: We know that,

 

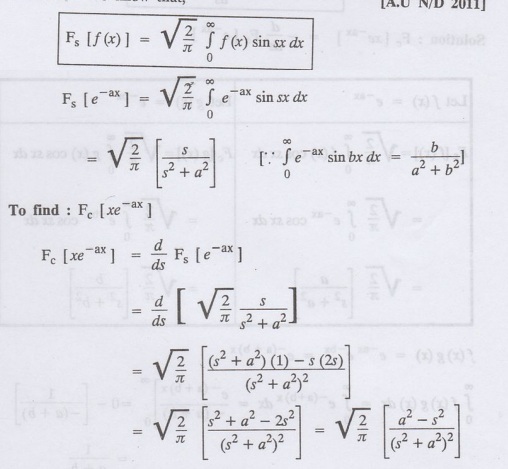
III (f) Problems based on Parseval's identity in F.S.T and F.C.T

 

Example 4.3.f(3): Using transform methods, evaluate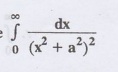 

Solution: Parseval's identity is

 

Example 4.3.f(5): Using Parseval's identity of the Fourier cosinetransform,Evaluates