Transforms And Partial Differential Equations: UNIT III: Application Of Partial Differential Equations
Finite Plates
Examples
Transforms And Partial Differential Equations: UNIT III: Application Of Partial Differential Equations:Examples
a. Finite Plates
Problems based on Finite PlatesType 1
Example
3.5a(1): A square plate is bounded by the lines x = 0, y=0, x = 1, y = 1. Its
faces are insulated. The temperature along the upper horizontal edge is given
by u(x, 1) = x(1-x) while the other three edges are kept at 0° C. Find the
steady state temperature in the plate.
Solution
:

Example
3.5a(2): Find the steady state temperature distribution in a rectangular plate
of sides a and b insulated at the lateral surface and satisfying the boundary
conditions
u (0, y) = u(a, y) = 0 for 0 ≤ y ≤b
u (x, b) = 0 and u (x, 0) = x (a - x) for 0 ≤x≤ a

Example
3.5a(3): The boundary value problem governing the steady - state temperature
distribution in a flat, thin, square plate is given by

Type
2. Finite plate with value given in y direction :

Problems
based on Finite Plates Type 2
Example
3.5a(4): A square plate is bounded by the lines x = 0, x=a, y= 0, y = a, of a
square plane bounded by the lines x = 0, y = 0, y = a are kept at temperature
0° C. The side x = a is kept at = 100, 0 < y < a. temperature given by u
(a, y) = 100, 0 <y< a.

Example
3.5a(5): A square plate is bounded by the lines x = 0, x=a, y = 0, y = = a of a
square plane bounded by the lines x = a, y = 0, y = a are kept at temperature
0° C. The side x = 0 is kept at temperature given by u (0, y) = 100, 0 < y
< a. Find u (x, y).

Problems based on Finite Plates:
Type 3. (Combination of Type 1 & Type 2)
Example 3.5a(6): A rectangular plate is bounded by the lines x = 0,. y = 0, x = a and y = b. It's surfaces are insulated and the temperature along two adjacent edges are kept at 100° C, while the temperature along the other two edges are at 0° C. Find the steady state temperature at any point in the plate. Also find the steady state temperature at any point of a square plate of side 'a' if two adjacent edges are kept 'a' if two (0,2)(iv) at 100° C and the others at 0° C.
Solution:

Now, we split the solutions into
two solutions.
i.e., u (x, y) = u1(x,
y) + u2 (x, y)
where u1(x, y) and u2
(x, y) are solutions of (1) and further u1 (x, y) is the temperature at any
point P with the edge BC maintained at 100° C and the other three edges at 0° C
where u2 (x, y) is the temperature at P with the edge AB maintained at 100°
other three edges at 0° C.
Therefore, the boundary conditions
for the functions u1 (x, y) and u2 (x, y) are as follows.
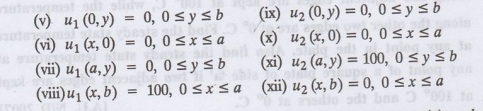
Clearly, both u1 and u2
satisfy the choosing the suitable solution we have,

b) Infinite Plates
PROBLEMS
ON INFINITE PLATES
Example
le 3.56(1): A rectangular plate with with insulated surface is 10 cm wide, so long
compared to its width that it may be considered infinite in length. If the
temperature at the short edge y = 0 is given by u = x for 0 ≤ x ≤ 5 and 10-x
for 5 < x < 10 and the two long edges x 0, x = 10 as well as the other
short edge are kept at 0° C. Find the temperature function u (x, y) at any
point of the plate.
Solution:
The equation to be solved is

Example 3.5b(2) : A rectangular
plate with insulated surface is 10 cm wide and so long compared to its width
that it may be considered infinite in length without introducing an appreciable
error. If the of the short edge y = 0 is given by 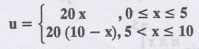 and the
two long edges x = 0 and x = 10 as well as the other short edge are at 0° C.
Prove that the temperature, u (x, y) at any point (x, y) of the plate is given
by
and the
two long edges x = 0 and x = 10 as well as the other short edge are at 0° C.
Prove that the temperature, u (x, y) at any point (x, y) of the plate is given
by
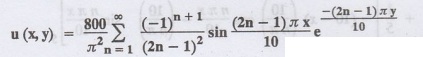
Proof:
Let u(x, y) be the temperature at any point (x, y) in the steady state. Then u
satisfies the differential equation 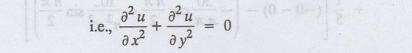
From the given problem, we get the
following boundary conditions
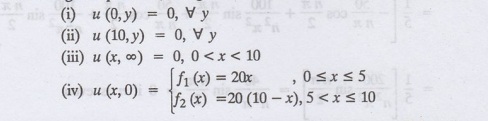
Now, the suitable solution which
satisfies our boundary conditions is given by

Equations from (1) to (5) is same
as Example No. 3.5b(1)
The most general solution is
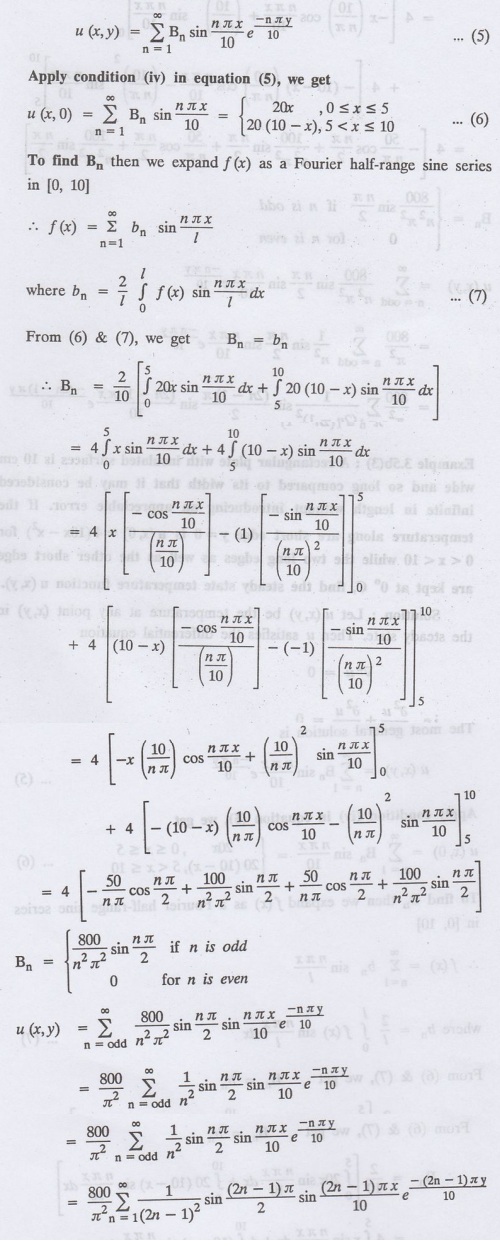
Example
3.5b(3): A rectangular plate with insulated surfaces is 10 cm wide and so long
compared to its width that it may be considered infinite in length without
introducing an appreciable error. If the temperature along are short edge y = 0
is u(x, 0) = 4 (10x - x2) for 0 < x < 10 while the two long
edges as well as the other short edge are kept at 0° C, find the steady state
temperature function u (x, y).
Solution: Let u(x, y) be the temperature at any point (x, y) in the steady state. Then u satisfies the differential equation

Horizontal plate
Example
3.5b(4): An infinitely long rectangular plate with insulated surface is 10 cm
wide. The two long edges and one short edge are kept at zero temperature, while
the other short edge x = 0 is kept at temperature given by u (0, y)
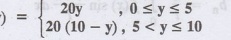
Find the steady state temperature
distribution in the plate.
Solution:
The equation to be solved is 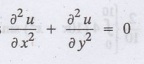
From the given problem, we get the
following boundary conditions

Example 3.5b(5) : A rectangular plate with insulated surface is 8 cm wide and so long compared to its width that it may be considered infinite in length without introducing an appreciable error. If the temperature along the short edge y = 0 is given by u (x, 0) = 100 sin in 0 < x < 8, while the long two edges x=0 and x = 8 as well as the other short edge are kept at 0° C, find the steady state temperature function u (x, y).

Transforms And Partial Differential Equations: UNIT III: Application Of Partial Differential Equations : Tag: : Examples - Finite Plates