Exercise

EXERCISE 3.3(a).

1. A uniform elastic string of length 60 cm is subjected to a constant tension of 2 kg. If the ends are fixed and the initial displacement is y (x, 0) 60x - x² for 0 < x <60 while the initial velocity is zero, find the displacement function y (x, t).

2. A tightly stretched string with fixed end points x = 0 and x = 1 is initially in a position given by 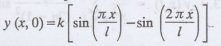 If it is released from rest from this position find the displacement y at any distance x from one end at any time t.

3. A taut string of length 21 is fastened at both ends. The mid point of the string is taken to a height h and then released from rest in that position. Find the displacement of the string.

4. The points of trisection of a tightly stretched string of length 30 cm with fixed ends pulled aside through a distance of 1 cm on opposite sides of the position of equilibrium and the string is released from rest. Find an expression for the displacement of the string at any subsequent time, also show that the mid points of the string remains always at rest.

5. A string of length is fastened at both ends. One end is taken as the origin and at a distance b from this end, the string is displaced a distance d transversely and is released from rest when it is in this position. Find the equation of the sub-sequent motion.

6. A tightly stretched flexible string has its ends fixed at x = 0 and x=1. At time t = 0 the string is given a shape defined by f(x)=ux (1-x) where μ is a constant and then released. Find the displacement of the string at any time 't'.

ANSWERS