Transforms And Partial Differential Equations: UNIT II: Fourier Series
Exercise
Transforms And Partial Differential Equations: UNIT II: Fourier Series: Exercise
EXERCISE 2.4
1.
Find the complex form of the Fourier series of the periodic function f(x) =
sinx, 0 < x <л.
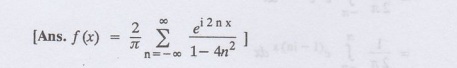
2.
Find the complex form of the Fourier series of f (x) = cos ax in -л <x<л,
where a is not an integer.
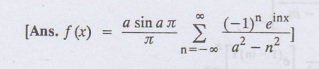
3.
Obtain the complex form of the Fourier series for
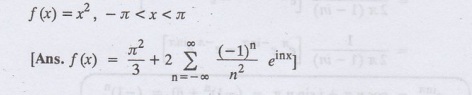
4.
Find the complex form of the Fourier series of f (x) = sin ax where a is not an
integer in - л <x<л.
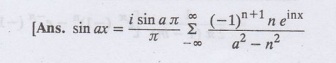
5.
Prove that the complex form of the Fourier series f(x) = cos zx in - л < x
<л where a is not an integer, is given by
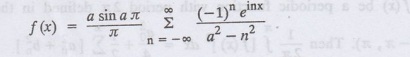
6.
Find the complex form of Fourier series of
Transforms And Partial Differential Equations: UNIT II: Fourier Series : Tag: : - Exercise
Transforms And Partial Differential Equations: UNIT II: Fourier Series
Under Subject
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Materials and Metallurgy
ME3392 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Manufacturing Processes
ME3393 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation