Transforms And Partial Differential Equations: UNIT II: Fourier Series
Exercise
Transforms And Partial Differential Equations: UNIT II: Fourier Series: Exercise
EXERCISE 2.3
1.
Express as a Fourier Sine Series
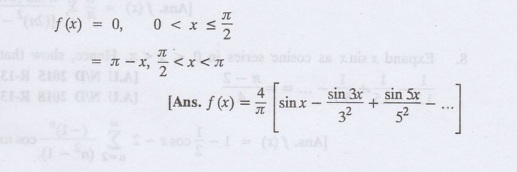
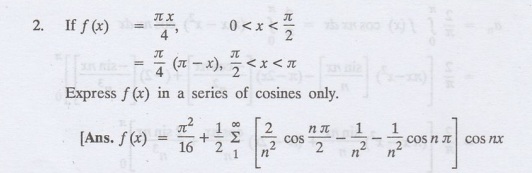
3.
Find a Fourier sine series for f (x) = k in 0 < x < л
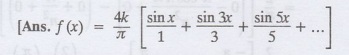
4.
Find the Fourier cosine series, and Fourier sine series for
5.
Find the Fourier sine series for f (x) =ax + b in 0 < x <
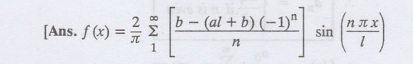
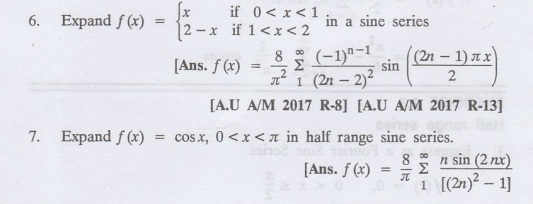
8.
Expand x sinx as cosine series in 0 < x <л. Hence, show that
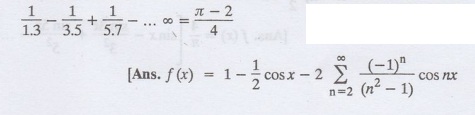
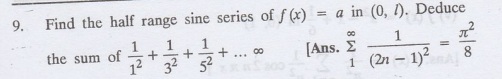
10.
Find the half range sine series of f (x) = sin ax in (0, l)
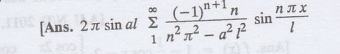
11.
Find the half range cosine series for
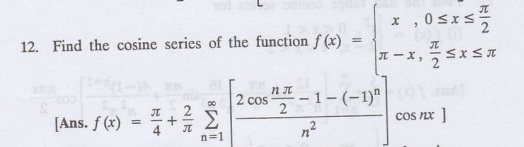
13.
Obtain the half range cosine series for f (x)= cosh ax in 0<x<π
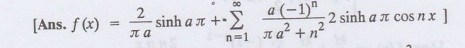
14.
Obtain the half range cosine series for f (x) = (x-2)2
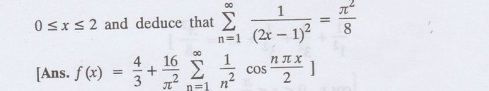
15.
Obtain the Fourier sine series for sinx in 0 <x<л
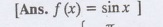
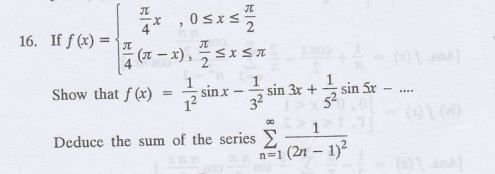
17.
Prove that in 0 < x < л
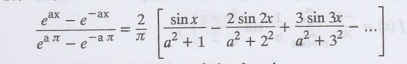
18.
Obtain the sine series of the function
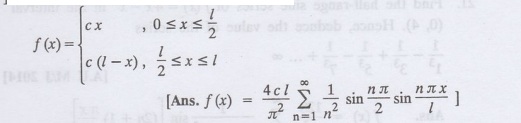
19.
Find the Fourier sine series for the function
20.
Find the half range sine series of
21.
Find the half-range sine series of of ƒ
(x) = 4x − x2 in the interval (0, 4). Hence, deduce the value of the
series
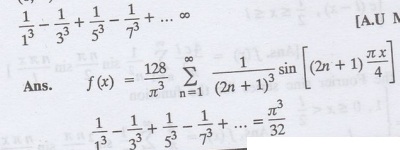
Transforms And Partial Differential Equations: UNIT II: Fourier Series : Tag: : - Exercise
Transforms And Partial Differential Equations: UNIT II: Fourier Series
Under Subject
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Materials and Metallurgy
ME3392 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Manufacturing Processes
ME3393 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation