Transforms And Partial Differential Equations: UNIT II: Fourier Series
Exercise
Transforms And Partial Differential Equations: UNIT II: Fourier Series: Exercise
Exercise 2.1.(a)
Problems under the interval (0, 2л)
1.
Show that in the range 0 to 2л the Fourier series expansion for
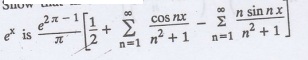
2.
Express f(x) = 1/ 12 (3x2-6xл+2л2) as a Fourier series of
period 2л in the interval (0, 2л). Hence, show that

3.
An alternating current after passing through a rectifier has the
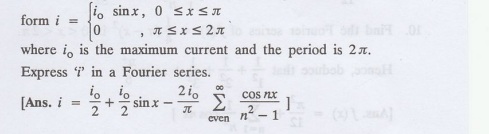
4.
Find the Fourier series of

5.
Expand f (x) = as a(л-x)2 as a Fourier series of period 2л in the 0
≤x≤2л when a is a constant.
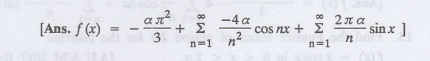
6.
Express f(x) = (л. -x)2 as a F.S of period 2л in the interval 0 < x < 2л.
Hence, deduce the sum of the series
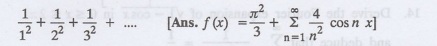
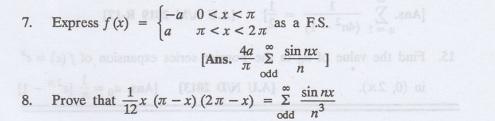

Transforms And Partial Differential Equations: UNIT II: Fourier Series : Tag: : - Exercise
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
