Transforms And Partial Differential Equations: UNIT II: Fourier Series
Examples
Transforms And Partial Differential Equations: UNIT II: Fourier Series: Examples
(a) PROBLEMS UNDER THE INTERVAL (0, 2 л)
Example
2.1.a(1): If f(x) = 1/2(л /x), find the Fourier series of period
2л in the interval (0,2 л). Hence deduce that
Example
2.1.a(2): Expand f(x) = x (2л-x) as Fourier series in (0, 2л) and hence deduce
that the sum of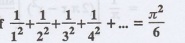 
Solution
: Given: f(x) = x (2л - x) = 2πx-x2
Let the required Fourier series be
Example
2.1.a(3) Determine the Fourier series for the function f(x)=x of period 2л in 0
< x < 2л.
Solution
:
Let the required Fourier series be
Example
2.1.a(4): Expand f(x) eax as a Fourier series in (0, 2 л).
Solution
:
Let the required Fourier series be
Example
2.1.a(5): Obtain the Fourier series of periodicity 2л for
Example
2.1.a (6): Expand in Fourier series of f(x) = x sin x for 0
< x < 2л and deduce the result
Example
2.1.a(7): Obtain the Fourier series for the function
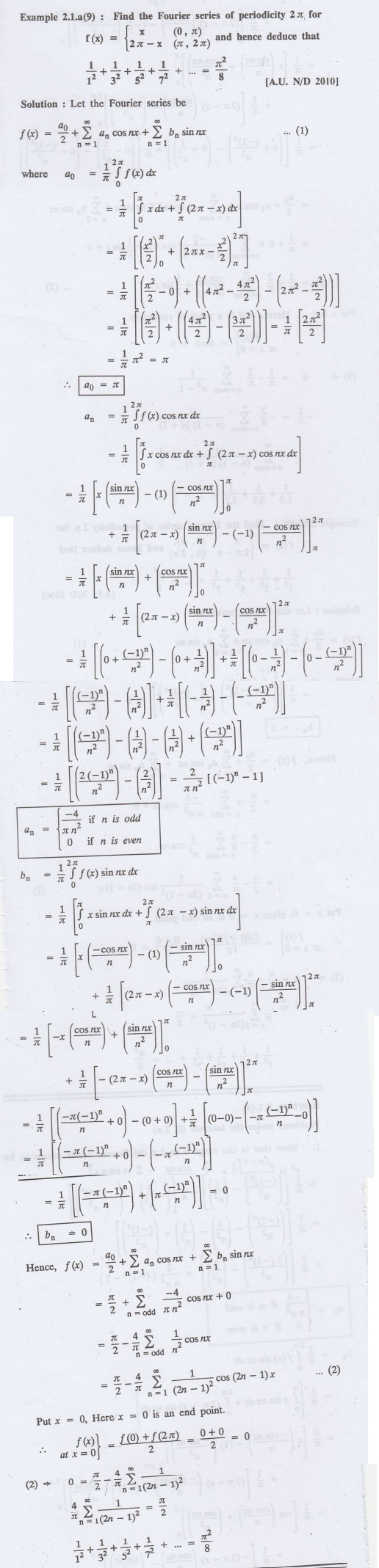
Transforms And Partial Differential Equations: UNIT II: Fourier Series : Tag: : - Examples
Transforms And Partial Differential Equations: UNIT II: Fourier Series
Under Subject
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Materials and Metallurgy
ME3392 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Manufacturing Processes
ME3393 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation