Transforms And Partial Differential Equations: UNIT II: Fourier Series
Examples
So sinx is a periodic function with the period 2л. This is alsoncalled Sinusoidal periodic function.
Example:
1. sin x = sin (x + 2л) = sin (x +
4л)= …
So sinx is a periodic function with
the period 2л. This is alsoncalled Sinusoidal periodic function.
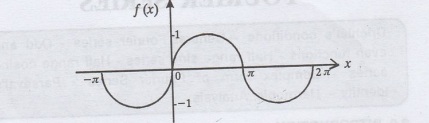
2. The trignometric functions sinx
and cosx are periodic functions with functions fundamental (primitive) period
2л.
3. sin 2x and cos 2x are also
periodic functions with fundamental period л.
4. tanx is a periodic function with
period л.
5. Find the period of sin nx where
n is a positive integer shoqmi od
Solution:
Let f (x) = sin nx = sin (nx + 2л)
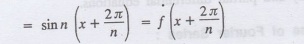
Therefore, 2л /n is the period of
sin nx, 2π/n is the period of coxnx π/n is the period of cos nx
6. Show that a constant has any
positive number as period.
Solution
:
Let f(x) = c, where is a constant.
Then f(x + k) = c, k being any
positive number
that is f(x + k) = f(x)
So f(x) is periodic with period k.
Note :
Since, there is no least value of k, we say that f(x) = c
has no fundamental period.
7. Let f : RR be the function
defined by

Let p be any rational number. If x
is rational, then x + p is also rational and if x is irrational, then x + p is
also irrational.

Hence, every rational number is a
period of f and ƒ has no fundamental period.
8. Let ƒ and g be periodic
functions with period p and let a and b be real numbers. Prove that af + bg is
also a periodic function with period p.
Solution: Since, ƒ and g are
periodic with period p
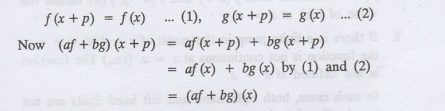
Hence, af + bg is periodic with
period p.
9. If p is a period of f (x), show
that np is also a period where n is any integer (positive or negative)
Solution:
Since
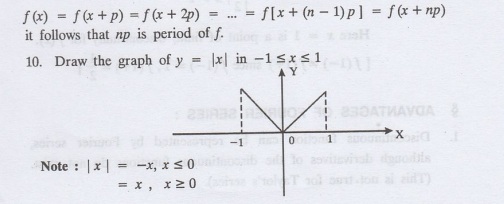
Transforms And Partial Differential Equations: UNIT II: Fourier Series : Tag: : - Examples
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
