Transforms And Partial Differential Equations: UNIT I: Partial Differential Equations
Examples
Transforms And Partial Differential Equations: UNIT I: Partial Differential Equations:Examples
Problems based on Non-homogeneous linear
equation
Example
1.5.34 : Solve (D + D' − 2) z = 0
Solution:
Given: (D + D' − 2) z = 0
i.e., [D-(-1) D' - 2] z = 0
We know that, working rule case (i)
is
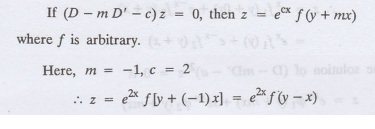
Example
1.5.35 : Solve (D+D' - 2) (D+ 4 D' - 3) z = 0
Solution:
Given: (D + D' - 2) (D + 4D' - 3) z = 0
i.e., (D − (−1) D' – 2 ][ D − (−4)
D' – 3] z = 0
We know that, working rule case
(ii) is
If (D-m1 D' - c1)
(D - m2 D' - c2) ... (D − mn D' — cn)
z = 0,
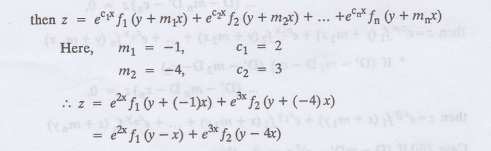
Example
1.5.36: Solve : (D2 - DD' + D' − 1) z = 0
Solution
:

Example
1.5.37 : Solve : (2 DD' + D'2 - 3D') z = 3 cos (3x – 2y)
Solution:
To find the complementary function

Example
1.5.38: Solve (D − D' − 1) (D − D' − 2) z = e2x—y
Solution
:
Given: (D − D' − 1) (D − D' − 2) z = e2x—y
To find C.F. take
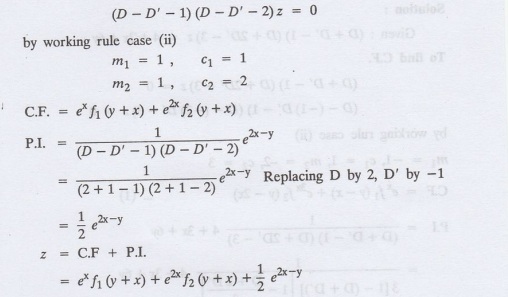
Example
1.5.39 : Solve (D − D' − 1) (D − D' − 2) z = e2x + y.
Solution
:
Given : (D - D' - 1) (D − D' − 2) z = e2x+y
To find C.F.
(D-D' - 1) (D-D' − 2) z = 0
by working rule case (ii)
m1 = 1, c1 = 1, c2
= 2, m2 = 1
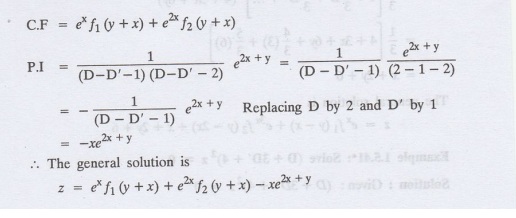
Example
1.5.40: Solve (D+ D' - 1) (D + 2D' - 3) z = 4+3x+6y.
Solution : Given (D+D' − 1)
(D + 2D' − 3) z = 4 + 3x + 6y
To find C.F.
(D+D' - 1) (D + 2D' - 3) z = 0
(D − (−1) D' - 1) (D − (−2) D' — 3) z = 0 = 0
by working rule case (ii)

Example
1.5.41: Solve (D + 3D' + 4)2 z =
Solution:
Given: (D+3D' + 4)2 z = 0

EXERCISES

Transforms And Partial Differential Equations: UNIT I: Partial Differential Equations : Tag: : - Examples
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
