Transforms And Partial Differential Equations: UNIT I: Partial Differential Equations

Examples

Formulae

Home | All Subjects | CIVIL Department | Transforms and Partial Differential Equations
Next >>

Transforms And Partial Differential Equations: UNIT I: Partial Differential Equations: Examples

R.H.S= sin (ax + by) or cos (ax + by)

Replace D2 by -a2, DD' by -ab, D/2 by -b2

Formulae



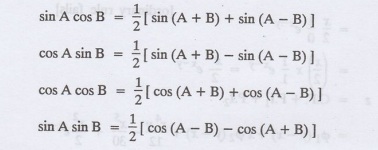
Example 1.5.19: Solve [D2 - 2DD' + 2D'2]  z = sin (x − y).

Solution: Given [D2 - 2DD' + 2D'2] z = sin (x -- y)

The auxiliary equation is m2 - 2m + 2 = 0

[Replace D m and D' by 1]


 

Example 1.5.20 : Solve [D3 - 4D2 D' + 4DD'2] z = 6 sin (3x+6y).

Solution: Given: [D3 – 4D2 D′ + 4DD'2] z = 6 sin (3x + 6y)

The auxiliary equation is m3 - 4m2 + 4m

 


Example 1.5.21 : Solve [D2 - 2DD' + D'2] z = cos (x-3y).

Solution: Given: [D2 - 2DD' + D'2]z = cos (x - 3y)

The auxiliary equation is m2 - 2m + 1 = 0

(m − 1)2 = 0

m = 1, 1

Replace D2 by −12=-1

| DD' by −(1) (−3) =3 D'2 by -(-3)2 = −9



Example 1.5.23: Solve [D2 - 3DD' + 2D'2] z= sin x cos y

Solution :

Given: [D2 - 3DD' + 2D'2] z= sin x cos y

The auxiliary equation is m2 - 3m + 2 = 0

M = 1, 2


Example 1.5.24: Solve (D2 - DD') 7- sin x sin 2y

Solution: Given: (D2 - DD') 7- sin x sin 2y

The auxiliary equation is


Transforms And Partial Differential Equations: UNIT I: Partial Differential Equations : Tag: : Formulae - Examples

Home | All Subjects | CIVIL Department | UNIT: Transforms and Partial Differential Equations
Next >>

Related Topics


Partial Differential Equations - Introduction

Formation of partial differential equations by elimination of arbitrary Constants

Problems based on formation of p.d.e by elimination of arbitrary constants (a.c.) - Partial Differential Equations

Exercise [formation of P.D.E by elimination of arbitrary constants (a.c.)] - Partial Differential Equations

Formation of partial differential equations by elimination of arbitrary functions

Solved Example Problems based on formation of p.d.e by elimination of arbitrary functions - Partial Differential Equations

Exercise [formation of p.d.e by elimination of arbitrary functions] - Partial Differential Equations

Solved Example Problems based on Formation of p.d.e by elimination of arbitrary functions - Partial Differential Equations

Exercise [Form the p.d.e by eliminating the arbitrary functions] - Partial Differential Equations

Singular Integrals - Solution of Standard Types of First Order Partial Differential Equations - Partial Differential Equations

Exercise [partial differential equation]

Methods to solve the first order partial differential equation

Solved Example Problems based on First order Partial Differential Equations (p.d.e)

Exercise [First order Partial Differential Equations]

Solved Example Problems based on Type 2 Clairaut's form z = = px + qy + f (p, q) - Partial Differential Equations

Related Subjects


Transforms and Partial Differential Equations

Transforms and Partial Differential Equations

MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation