Example Solved Problems and Exercise on p.d.e Type 3(a) Equation of the type f (z, p, q) = 0

Type 3 (a) Equation of the type f (z, p, q) = 0

i.e., equations not containing x and y.

Let z be a function of u where

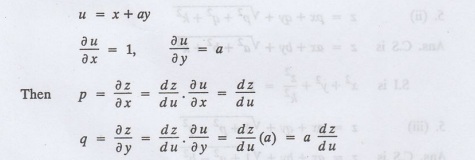
Substitute the values of P and q in the given equation f (z, p, q) =0, it becomes

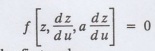 which is an ordinary differential equation of

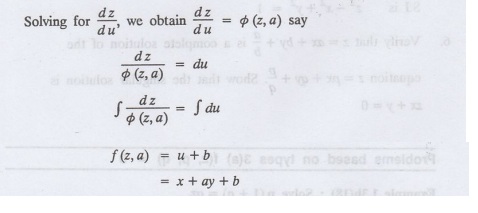
This is the complete integral, singular and general integral are found out as usual.

Rule: Assume u = x + ay; replace p and q by ppppppppppppp the given equation and then solve the ordinary diff. Equation to. obtained.

Type 3 (b) Equation of the type f (x, p, q) = 0 ... (1)

i.e., equations not containing y and z.

Let z is a function of x and y

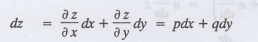
Assume that, q = a

Then the equation becomes f(x, p, a) = 0

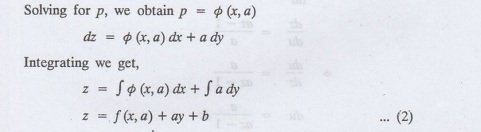
equation (2) is the complete integral of (1) since it contains two arbitrary constants a & b.

Type 3 (c) Equation of the type f (y, p, q) = 0 ………(1)

i.e., equations not containing x and z. Assume, pa and proceed as Type 3 (b)

The complete integral will be of the form z = ax + f (y, a) + b

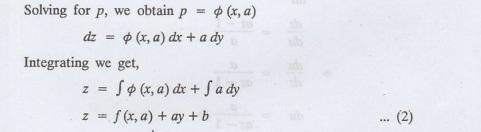
Problems based on types 3(a) f(z, p, q) = 0

Example 1.3b(18): Solve p (1 + q) = qz.

Solution: Given: p (1 + q):

Example 1.3b(19): Solve p (1+ q) = q(z − a)

Solution: Given: p (1 + q2) = q (z − a)

This equation is of the form f (z, p, q)  = 0

Example 1.3b(20): Solve z2 =1+ p2 + q2.

Solution: Given: z2 = 1+p2 + q2

The given problem is, of the type f (z, p, q) = 0

Since, the number of a.c. = number of I.V

General integral can be found out in a usual way.

Example 1.3b(21): Solve 9 (p2 + q2) = 4.

Solution: Given: 9 (p2 + q2)

This equation is of the form f (z, p, q)

Since, the number of a.c. = number of I.V

General integral can be found out in a usual way.

Example 1.3b(22) : Solve z = p2 + q2.

Solution: Given: z = p2 + q2

This equation is of the form f (z,p,q) = 0

Since, the number of a.c. = number of I.V

General integral can be found out in a usual way.

Example 1.3b(23): Solve Ap+ Bq + Cz = 0.

Solution: Given Ap + Bq + Cz = 0

This is of the form f (z, p, q) = 1

Example 1.3b(24): Solve p(1 − q2) q (1-z).

Solution: Given: p (1 − q2) = q (1 − z) ... (1)

This equation is of the form f (z, p, q) = 0

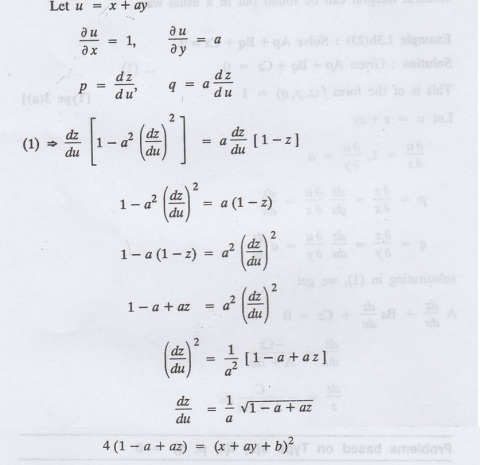
which gives the complete integral of the given equation.

Since, the number of a.c. = number of I.V

General integral can be found out in a usual way.

EXERCISE 1.3(b) - Type 3 (Case i) f(z, p, q) = 0

Find the complete integrals of the following :