Definition

FOURIER SERIES

Periodic functions occur frequently in engineering problems. Such periodic functions are often complicated. It is therefore desirable to represent these in terms of the simple periodic functions of sine and cosine.

Definition: Fourier Series:

Here, we express a non-sinusoidal periodic function into a fundamental and its harmonics, a series of sines and cosines of an angle and its multiples of the form.

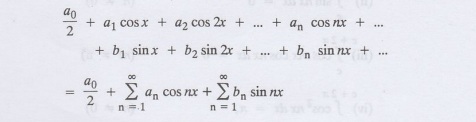
is called the Fourier series, where

a₀, a₁, a₂,……… an b₁, b₂, b_n,…………are constants. 

§ EULER'S FORMULA FOR THE FOURIER COEFFICIENTS

If a function f(x) defined in c <x<c + 2л can be expanded as the infinite trigonometric series,

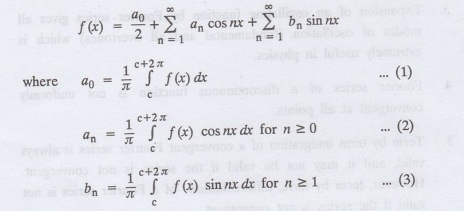
Formula (1), (2) and (3) are known as the Euler formulas.

Note: Only if the constant term is taken as a₀/2 formula (2) is true for n = 0.

§ Useful Integrals to establish Euler formulae :

To establish Euler formulae, the following integrals will be required.

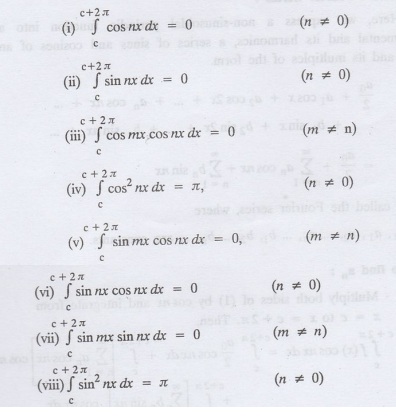
§ DETERMINATION OF FOURIER COEFFICIENTS : (Euler's Formulae)

Let f (x) be represented in the interval (c, c + 2л) by the Fourier Serics

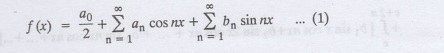
To find the coefficients of a_o, a_n and b_n.

We assume that the series (1) can be integrated term by term x = c to x = c + 2л

To find a₀:

Integrate both sides of equation (1) from

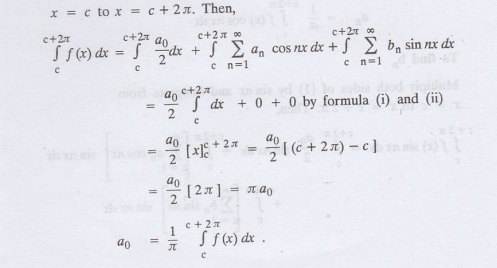
To find a_n:

Multiply both sides of (1) by cos nx and integrate from

To find b_n

Multiply both sides of (1) by sin nx and integrate from

x = c to x = c + 2л. Then,

§ CHANGE OF INTERVAL

In practice, we often require to find a Fourier series for an interval which is not of length 2л.

In many problems, the period of the function to be expanded is not 2л, but some other interval say 2l.

Suppose f (x) is defined in the interval (-l, l).