CPM and Pert Network Modelling and Time Analysis

CPM AND PERT NETWORK MODELLING AND TIME ANALYSIS

Any project involves planning, scheduling and controlling a number of interrelated activities with use of limited resources like, men, machines, materials, money and time. The projects may be extremely large and complex such as construction of a power plant, a highway, a shopping complex, ships and aircraft. It is required that managers must have a dynamic planning and scheduling system to produce the best possible results and also to react immediately to the changing conditions and make necessary changes in the plan and schedule.

A convenient analytical and visual technique of PERT and CPM prove extremely valuable in assisting the managers in managing the projects. PERT and CPM are basically time-oriented methods in the sense that they both lead to determination of a time schedule for the project. The significant difference between two approaches is that CPM is an activity oriented network while PERT is event oriented. CPM has single time estimate which is assumed to be deterministic and PERT has three time estimates for activities and uses probability theory to find the chance of reaching the scheduled time.

NETWORK DIAGRAM REPRESENTATION

In a network representation of a project the following representations are used:

Activity: Any individual operation which utilizes resources and has an end and a beginning is called activity. An arrow is commonly used to represent an activity with its head indicating the direction of progress in the project.

Here 'A' is the activity. These are classified into four categories:

(i) Predecessor activity - Activities that must be completed immediately prior to the start of another activity are called predecessor activities.

(ii) Successor activity - Activities that cannot be started until one or more of other activities are completed but immediately succeed them are called successor activities.

(iii) Concurrent activity - Activities which can be accomplished concurrently are known as concurrent activities. It may be noted that an activity can be a predecessor or a successor to an event or it may be concurrent with one or more of other activities.

(iv) Dummy activity An activity which does not consume any kind of resource and time is called a dummy activity. Dummy activities are simply used to represent a connection between events in order to maintain logic in the network. It is represented by a dotted line in a network.

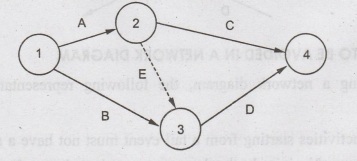
In the above example, A and B are preceding activities. C is dependent on activity A and D is dependent on activity B. Also A and B are concurring activities, since they are starting at the same time. Activity E is the dummy activity and it is marked as dotted line.

❖ Event: An event represents a point in time signifying the completion of some activities and the beginning of new ones. This is usually represented by a circle in a network which is also called a node or connector.

Here '1' and '2' are called events. 1 is the tail event and 2 is the head event. The events are classified in to three categories:

(i) Merge event - When more than one activity comes and joins an event such an event is known as merge event.

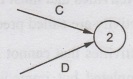
(ii) Burst event - When more than one activity leaves an event such an event is known as burst event.

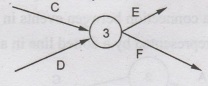
(iii) Merge and Burst event - An event may be merge and burst event at the same time as with respect to some activities it can be a merge event and with viorespect to some other activities it may be a burst event.b

 

ERRORS TO BE AVOIDED IN A NETWORK DIAGRAM

While drawing a network diagram, the following representations should be avoided:

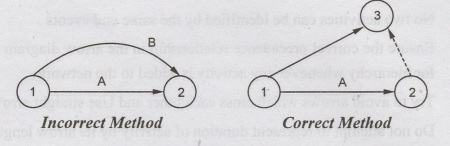
(i) Two activities starting from a tail event must not have a same end event. To ensure this, it is absolutely necessary to introduce a dummy activity.

(ii) Looping error should not be formed in a network, as it represents performance of activities repeatedly in a cyclic manner.

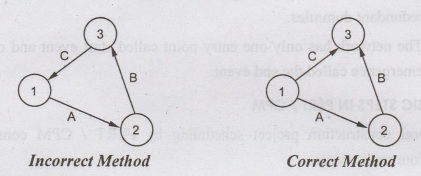
(iii) Dangling: To disconnect an activity before the completion of all activities in a network diagram is known as dangling. As shown in the figure activities (59) and (6-7) are not the last activities in the network. So the diagram is wrong and indicates the error of dangling

 

RULES FOR DRAWING NETWORK DIAGRAM

For a perfect network diagram, the following rules should be followed:

❖ Each activity is represented by one and only one arrow in the network

❖ No two activities can be identified by the same end events

❖ Ensure the correct precedence relationship in the arrow diagram and check for hierarchy whenever any activity is added to the network

❖ Try to avoid arrows which cross each other and Use straight arrows

❖ Do not attempt to represent duration of activity by its arrow length

❖ Use arrows from left to right. Avoid mixing two directions, vertical and standing arrows may be used if necessary.

❖ Use dummies freely in rough draft but final network should not have any redundant dummies.

❖ The network has only one entry point called start event and one point of emergence called the end event.

 

BASIC STEPS IN PERT / CPM

In general construction project scheduling by PERT / CPM consists of the following four main steps:

(i) Planning: The planning phase is started by splitting the total project in to small projects. These smaller projects in turn are divided into activities and are analyzed by the department or section. The relationship of each activity with respect to other activities are defined and established and the corresponding responsibilities and the authority are also stated. Thus the possibility of overlooking any task necessary for the completion of the project is reduced substantially.

(ii) Scheduling: The ultimate objective of the scheduling phase is to prepare a time chart showing the start and finish times for each activity as well as its relationship to other activities of the project. Moreover the schedule must pinpoint the critical path activities which require special attention if the project is to be completed in time. For non-critical activities, the schedule must show the amount of slack or float times which can be used advantageously when such activities are delayed or when limited resources are to be utilized effectively.

(iii) Resource allocation: Allocation of resources is performed to achieve the desired objective. A resource is a physical variable such as labour, finance, equipment and space which will impose a limitation on time for the project. When resources are limited and conflicting, demands are made for the same type of resources a systematic method for allocation of resources become essential. Resource allocation usually incurs a compromise and the choice of this compromise depends on the judgment of managers.

(iv) Controlling: The final phase in project management is controlling. Critical path methods facilitate the application of the principle of management by expectation to identify areas that are critical to the completion of the project. By having progress reports from time to time and updating the network continuously, a better financial as well as technical control over the project is exercised. Arrow diagrams and time charts are used for making periodic progress reports. If required, a new course of action is determined for the remaining portion of the project.

In addition to these basic steps essentially, there are six steps which are common to both the CPM and PERT techniques. They are listed as follows:

(i) Define the Project and all of its significant activities or tasks. The Project (made up of several tasks) should have only a single start activity and a single finish activity.

(ii) Develop the relationships among the activities. Decide which activities must precede and which must follow others.

(iii) Draw the "Network" connecting all the activities. Each Activity should have unique event numbers. Dummy arrows are used where required to avoid giving the same numbering to two activities.

(iv) Assign time and/or cost estimates to each activity

(v) Compute the longest time path through the network. This is called the critical path.

(vi) Use the Network to help plan, schedule, and monitor and control the sonog project.

 

CRITICAL PATH METHOD IN NETWORK ANALYSIS

Critical Path Method (CPM) was developed in the late 1950s as a method to resolve the issue of increased costs due to inefficient scheduling. Since then, CPM has become popular for planning projects and prioritizing tasks. It helps to break down complex projects into individual tasks and gain a better understanding of the project's flexibility. The Key Concept used by CPM is that a small set of activities, which make up the longest path through the activity network control the entire project. Such activity is called as critical activity. A critical path in project management is the longest sequence of activities that must be finished on time in order for the entire project to be complete. Any delays in critical tasks will delay the rest of the project. Non-critical activities can be re-planned, rescheduled and resources for them can be reallocated flexibly, without affecting the whole project. CPM revolves around discovering the most important tasks in the project timeline, identifying task dependencies, and calculating task durations. CPM has single time estimate which is assumed to be deterministic.

Basic Scheduling Computations in CPM

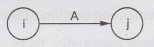
The basic notations used in CPM can be explained as follows:

For the given example,

(i,j) = Activity "A" with tail event "i" and head event "j”

 E_i = Earliest occurrence time of event i

E_j  = Latest al owable occurrence time of event j

D _{i j} = Estimated completion time of activity (i, j)

(E_S)_U = Earliest starting time of activity (i, j)

(E_F) _{i j}  = Earliest finishing time of activity (i, j)

(L_S) _{i j}   = Latest starting time of activity (i, j)

(L_f)_ij = Latest finishing time of activity (i, j)

(i) Determination of Earliest time (E_j): Forward Pass computation

Step 1

The computation begins from the start node and move towards the end node. For easiness, the forward pass computation starts by assuming the earliest occurrence time of zero for the initial project  event.

Step 2

Earliest starting time of activity (i, j) is the earliest event time of the tail end event

 i.e. (E_s)_ij = E_i

Earliest finish time of activity (i, j) is the earliest starting time + the activity time

i.e. (E_f)_ij = (E_s)_ij + D_ij or (E_f)_ij = E_i + D_ij

Earliest event time for event j is the maximum of the earliest finish times of all activities ending in to that event

i.e. E_j = max [(E_f)_ij for all immediate predecessor of (i, j)] or

E_j = max [E_i + D_ij]

(ii) Backward Pass computation (for latest allowable time)

Step 1

For ending event assume E = L.

Also all E's have been computed by forward pass computations.

Step 2

Latest finish time for activity (i, j) is equal to the latest event time of event j.

i.e. (L_f)_ij = L_j

Step 3

Latest starting time of activity (i, j) = the latest completion time of (i, j) - the activity time bollo ons omisioak

i.e. (L_s)_ij = (L_f)_ij - D_ij or (L_s)_ij = L_j - D_ij

Step 4

Latest event time for event '' is the minimum of the latest start time of all activities originating from that event

i.e. L_i = min [(L_s)_ij for all immediate successor of (i, j)] min [L_f )_ij- D_ij] = min [L_j – D_ij]

(iii) Determination of floats and slack times

There are three kinds of floats as follows:

❖ Total float - The amount of time by which the completion of an activity could be delayed beyond the earliest expected completion time without affecting the overall project duration time.

(T_f) _ij Latest start - Earliest start) for activity (i −j)

i.e. = (T_f) _ij  = (L_s)_ij - (E_s)_ij or (T_f)_ij = (T_L-T_E) - t_ij

❖ Free float The time by which the completion of an activity can be delayed beyond the earliest finish time without affecting the earliest start of a subsequent activity.

 (F_f) _ij =   Total float - Head event slack

i.e. (F_f ) = (E_j –E_i) -t_ij

❖ Independent float - The amount of time by which the start of an activity can be delayed without effecting the earliest start time of any immediately following activities, assuming that the preceding activity has finished at its latest finish time. The negative independent float is always taken as zero.

(I_f)_ij = Free float - Tail event slack

i.e. (I_f)_ij  =  (E_j - L_i) - t_ij

❖ Event slack - It is defined as the difference between the latest event and earliest event times.

Head event slack = L_j - E_j

Tail event slack = L_i - E_i

(iv) Determination of critical path

❖ Critical event - The events with zero slack times are called critical events. In other words the event i is said to be critical if E_i = L_i

❖ Critical activity - The activities with zero total float are known as critical activities. In other words an activity is said to be critical if a delay in its start will cause a further delay in the completion date of the entire project.

❖ Critical path - The sequence of critical activities in a network is called critical path. The critical path is the longest path in the network from the starting event to ending event and defines the minimum time required to complete the project.

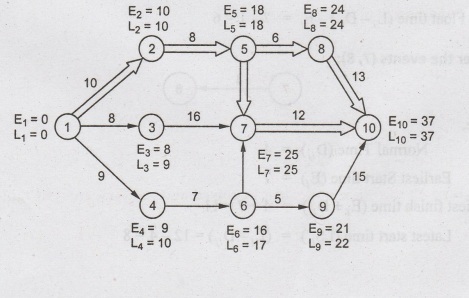
Example 1 :

Determine the early start and late start in respect of all node points and identify critical path for the following network.

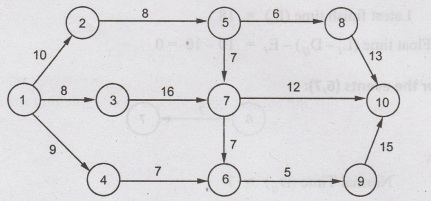
Solution:

In the networks shown, there are many paths by which the last event can be achieved.

Consider the events (1, 3):

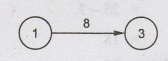
Here,

Normal Time (D_ij) = 8

Earliest Start time (E_i) = 0   (Event 1 has no preceding event E_i = 0)

Earliest finish time (E_i + D_ij) = 0+8=8

Latest start time (LS_ij) = (L_i-D_ij) = 9-8=1

Latest finish time (L_i) = 9

Float time (L_i -D_ij) – E_i = 1-0 = 1

Consider the events (2,5):

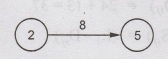
Here,

Normal Time (D_ij) = 8

Earliest Start time (E_i) = 10

Earliest finish time (E_i + D_ij) = 10+8 =18

Latest start time (LS_ij) =   (L_i- D_{i j})  = 18-8=10

Latest finish time (L_i) = 18

Float time (L_i-D_ij) - E_i  = 10-10 = 0

Consider the events (6,7):

Normal Time (D_ij) = 7

Earliest Start time (E_i) = 16

Earliest finish time (E_i + D_ij) = 16+7 =23

Latest start time (LS_ij) =   (L_i- D_{i j})  = 25-7=18

Latest finish time (L_i) = 25

Float time (L_i - D_ij) - E_i  = 18-16 = 2

Consider the events (8, 10):

Here,

Normal Time (D_ij) = 13

Earliest Start time (E_i) = 24

Earliest finish time (E_i + D_ij) = 24+13 =37

Latest start time (LS_ij) =   (L_i- D_{i j})   =37-13=24

Latest finish time (L_i) = 37

Float time (L_i - D_ij) - E_i  = 24-24 = 0

Likewise all the other nodes can be solved and network analysis table can be

Network Analysis Table

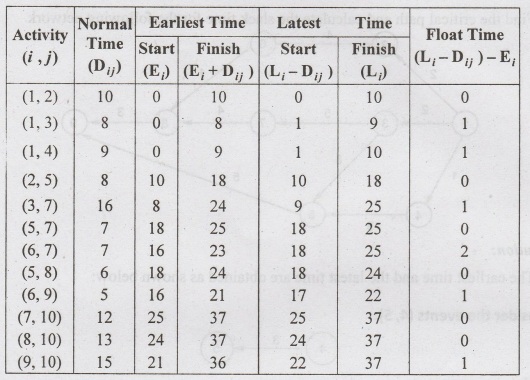
From the table, the critical nodes are (1, 2), (2, 5), (5, 7), (5, 8), (7, 10) and (8, 10)

From the table, there are two possible critical paths

(i) 1→2→5→ 8 → 10

(ii) 1→2→ 5→710

Calculation of E and L for each node is shown in the network below:

Example 2

Find the critical path and calculate the slack time for the following network

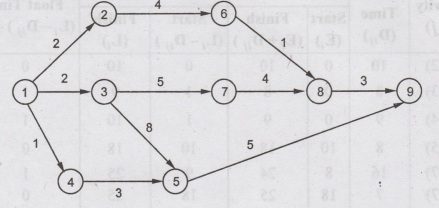
Solution:

The earliest time and the latest time are obtained as shown below:

Consider the events (4, 5):

Here,

Normal Time (D_ij) = 3

Earliest Start time (E_i) = 1

Earliest finish time (E_i + D_ij) =  3 + 1  = 4

Latest start time (LS_ij) =   (L_i- D_{i j})   = 10- 3 = 7

Latest finish time (L_i) = 7

Float time (L_i - D_ij) - E_i  = 7 - 1 = 6

Consider the events (7, 8):

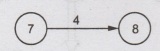
Here,

Normal Time (D_ij) = 4

Earliest Start time (E_i) = 7

Earliest finish time (E_i + D_ij) =  4 + 7 = 11

Latest start time (LS_ij) =   (L_i- D_{i j})   = 12-4= 8

Latest finish time (L_i) = 12

Float time (L_i - D_ij) - E_i  =  8 - 7 = 1

Consider the events (5, 9):

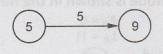
Here,

Normal Time (D_ij) = 5

Earliest Start time (E_i) = 10

Earliest finish time (E_i + D_ij) = 10+5 = 15

Latest start time (LS_ij) =   (L_i- D_{i j})   = 15-5 = 10

Latest finish time (L_i) = 15

Float time (L_i - D_ij) - E_i  = 10-10 = 0

Likewise all the other nodes can be solved and network analysis table can be framed:

Network Analysis Table

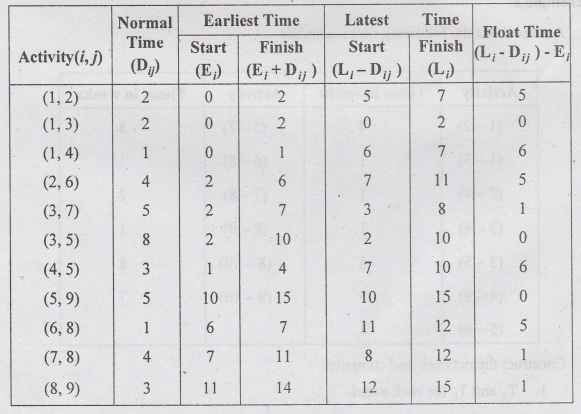
From the above table, the critical nodes are the activities (1, 3), (3, 5) and (5,9)

The critical path is 1→3→ 5→ 9

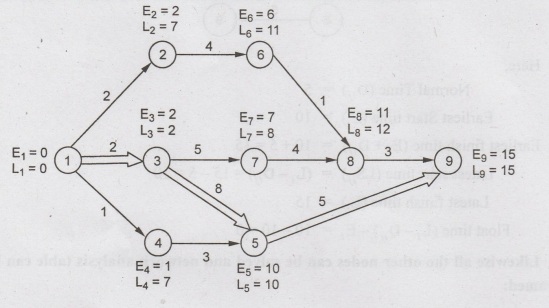
Calculation of E and L for each node is shown in the network below:

Example 3

A project has the following times schedule

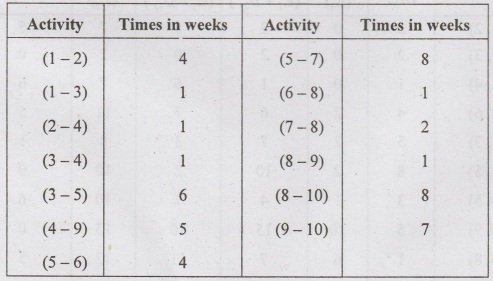
Construct the network and compute :

1. T_E and T_L for each event

2. Float for each activity

3. Critical path and its duration

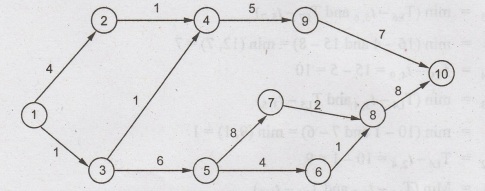
Solution:

The network diagram can be drawn as shown below:

To determine the critical path, the earliest time TE and latest time T1 for each of the TL

activity of the project is to be computed.

To calculate TE for all activities,

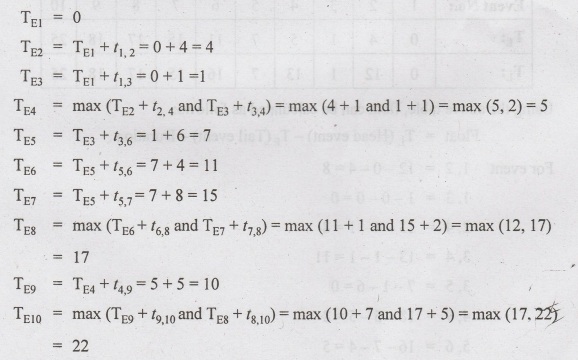
To calculate T, for all activities

TL10 = TE10 = 22

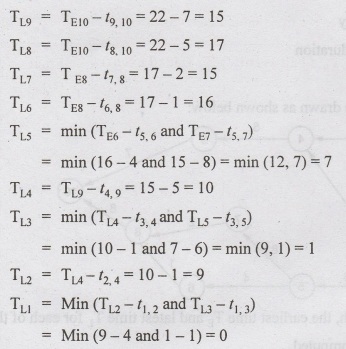
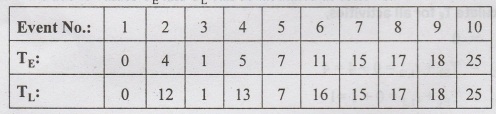
From the above values TE and T can be tabulated as follows:

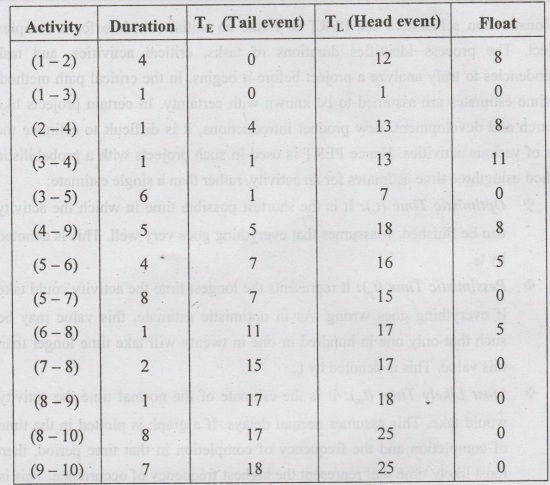
Using the above table, float can be calculated as follows:

Float = T_L (Head event) - T_E (Tail event) - Duration

For event 1,2 = 12-0-4=8

1,3 = 1-0-0=0

2,4 13-4-1=8

3,4 13-1-1=11

3,5 7-1-6=0

4,9 18-5-5=8

5,616-7-4=5

5,7 5-7-8=0

6-8 17-11-1=5

Likewise, the float for all events can be tabulated as follows:

Calculation of E and L for each node is shown in the network below

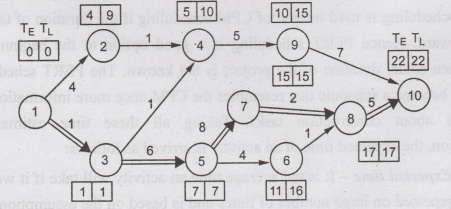
The resultant network shows the critical path

1→35→78→10

 
PROGRAM EVALUATION AND REVIEW TECHNIQUE (PERT) IN NETWORK ANALYSIS

Construction schedulers use PERT to create an initial schedule for a complex project. The process identifies durations of tasks, critical activities, and task dependencies to truly analyze a project before it begins. In the critical path method, the time estimates are assumed to be known with certainty. In certain projects like research and development, new product introductions, it is difficult to estimate the time of various activities. Hence PERT is used in such projects with a probabilistic method usingthree time estimates for an activity, rather than a single estimate:

❖ Optimistic Time (t_o): It is the shortest possible time in which the activity can be finished. It assumes that everything goes very well. This is denoted by to.

❖ Pessimistic Time (t_p) It represents the longest time the activity could take if everything goes wrong. As in optimistic estimate, this value may be such that only one in hundred or one in twenty will take time longer than this value. This is denoted by tp. (t):

❖ Most Likely Time (t_m): It is the estimate of the normal time the activity would take. This assumes normal delays. If a graph is plotted in the time of completion and the frequency of completion in that time period, then most likely time will represent the highest frequency of occurrence. This is denoted by tm.

PERT scheduling is used instead of CPM scheduling if the duration of tasks isn't straightforward. Hence PERT scheduling is a good option at the beginning of a project when actual duration of the project is not known. The PERT schedule may eventually become a schedule that resembles the CPM once more information can be determined about construction tasks. Taking all these time estimates into consideration, the expected time of an activity is arrived as follows:

❖  Expected time - It is the average time an activity will take if it were to be repeated on large number of times and is based on the assumption that the activity time follows Beta distribution, this is given by

t_e = (t_o +4 t_m + t_p)/6

❖ The variance for the activity is given by

σ ^{2 =} [(t_p-t₀)/6]²

Example 1

For the project shown in the figure

Find the earliest and latest expected time to each event and also critical path in the network.

Solution:

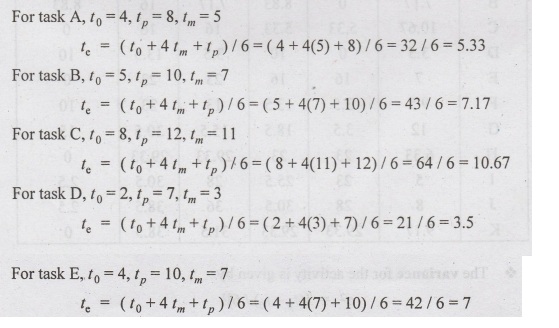
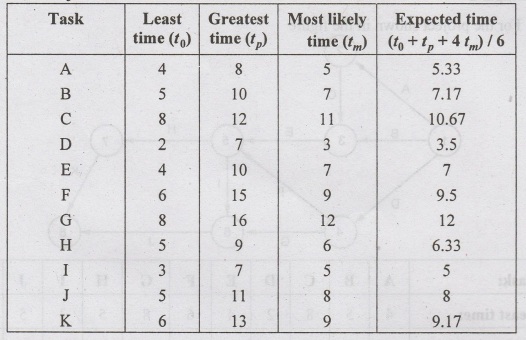
Likewise te for all the tasks can be calculated and tabulated as follows:

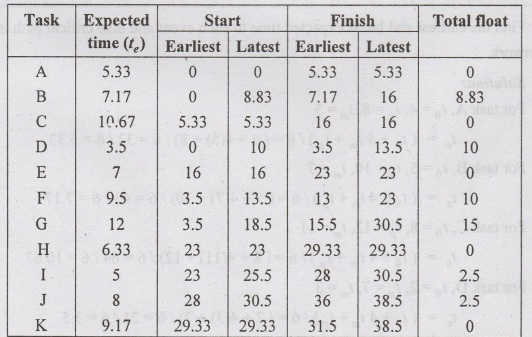
From the t_e calculated Earliest start time and Earliest finish time can be calculated as follows:

The network diagram can be drawn as shown below:

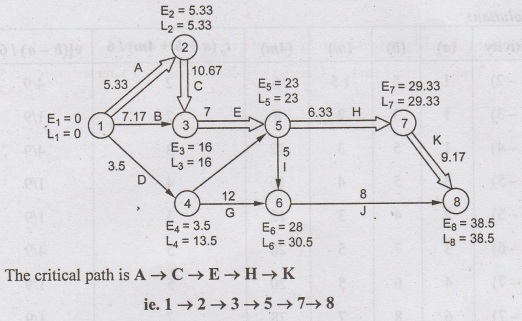
Example 2

A project has the following characteristics:

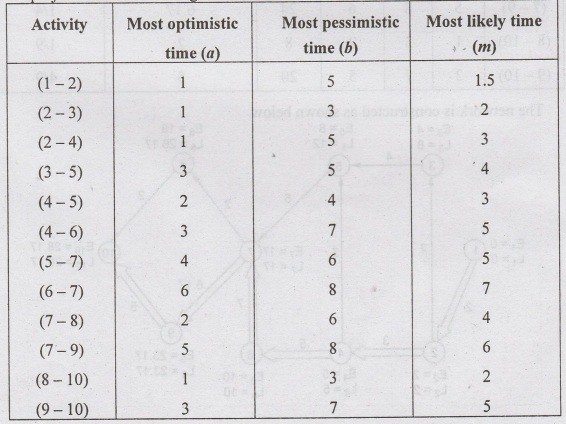
Construct a PERT network. Find the critical path and variance for each event.

Solution:

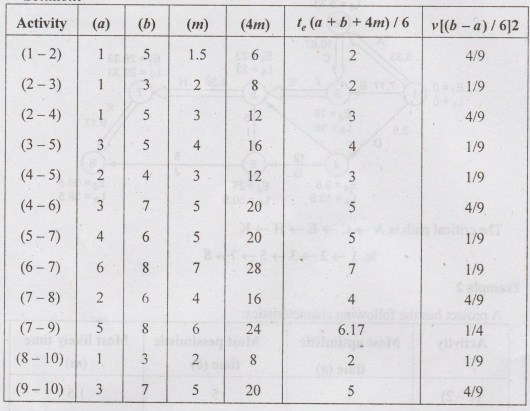
The network is constructed as shown below

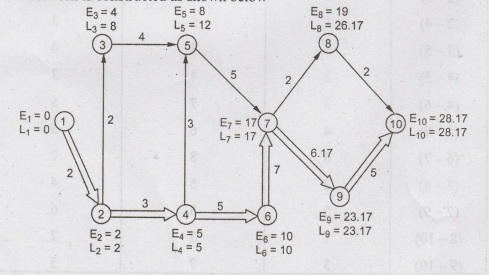
The critical path = 1→2→4→6-7-9-10

Example 3

Calculate the variance and the expected time for each activity

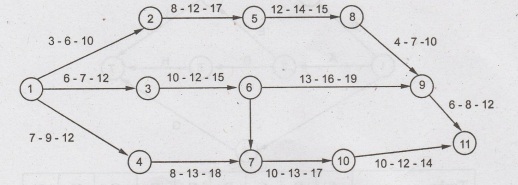
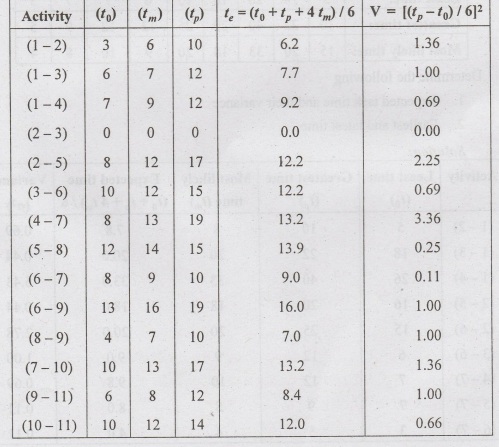
Example 4

A project is represented by the network as shown below and has the following

data

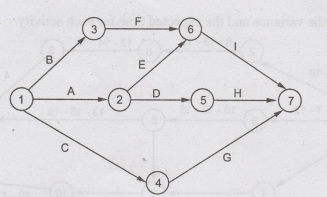
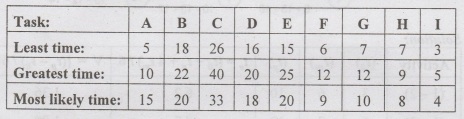
Determine the following

1. Expected task time and their variance

2. Earliest and latest time

Solution:

Activity Least time Greatest time

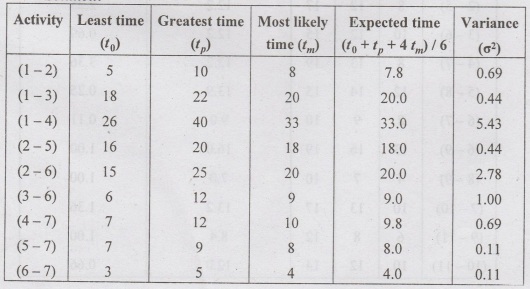
Earliest time can be calculated as follows:

E₁ = 0

E₂ = 0+7.8 7.8

E₃ = 0+20=20

E₄ = 0+33=33

E₅ = 7.8+18=25.8

E₆ = max [7.8 + 20, 20 + 9] = 29

E₇ = max [33 +9.8, 25.8+ 8, 29+ 4] = 42.8

Latest time can be calculated as follows:

L₇ = 42.8

L₆ = 42.8-438.8

L₅ = 42.8-8= 34.3

L₄ = 42.8 9.833

L₃ = 38.8-9 29.8

L₂ min [34.8-18, 38.8-20]= 16.8

L₁ = min [16.8-7.8, 29.8-20, 33-33]=0

 

 DIFFERENCE BETWEEN PERT AND CPM

❖ PERT is probabilistic in nature. It acknowledges and considers the variability in completion; times of activities and, in turn, the project. Accordingly it is useful for analyzing project scheduling problems with of bozu uncertain completion times of the activitiesinvolved.

❖ CPM is deterministic in nature. It is most appropriately used in projects in ubivib which activity durations are known with certainty. Not only the amount of

time needed to complete various facets of the project but also the amount of resources required for performing each of the activities are assumed to be known and certain.

❖ PERT is useful for projects that are new, non-repetitive, or which involve research and development while CPM is of great value for projects that are repetitive and standardized, like those involving construction activities

❖ PERT focuses primarily on time element and attaches lesser significance to the cost. CPM puts strong emphasis on cost and specifically considers the time-cost relationshipand trade-off.

❖ PERT is event oriented so that probabilities of reaching various events by certain dates may be calculated through event variances. CPM is activity oriented.

 

 ADVANTAGES AND DISADVANTAGES OF PERT AND CPM

PERT/CPM has the following advantages:

❖ A PERT/CPM chart explicitly defines and makes visible dependencies (precedence relationships) between the elements,

❖ PERT/CPM facilitates identification of the critical path and makes this visible,

❖ PERT/CPM facilitates identification of early start, late start, and slack for each activity,

❖ PERT/CPM provides for potentially reduced project duration due to better understanding of dependencies leading to improved overlapping of activities and tasks where feasible.

PERT/CPM has the following disadvantages:

❖ The lack of a timeframe on most PERT/CPM charts makes it harder to show status although colours can help (e.g., specific colour for completed nodes),

❖ When the PERT/CPM charts become unwieldy, they are no longer used to manage the project.

❖ There can be potentially hundreds or thousands of activities and individual dependency relationships will be complicated for big projects.