Continuity Of Function

§ CONTINUITY OF A FUNCTION:

The left hand limit of f (x) at x = a is defined as x approaches a from the left and is denoted by f (a −). a from the left and is denoted by f(a-)

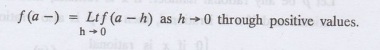
The right hand limit of f (x) at x = a is defined as x approaches a from the right and is denoted by f (a +)

A function f(x) is said to be continuous at x = f (a) = f (a) = f (-a)

Note: 1. ƒ(a) is different from ƒ (a +) rom ƒ (a +) and ƒ (a −), ƒ (a) means the value of f (x) at x = a.

2. If there is a finite jump in the graph of y = f (x) at x = a, the function is not continuous at x = a. (i.e.,) The function is not defined at x = a.

In such cases, both right hand and left hand limits are not equal. The function f(x) is piecewise continuous in an interval (a, b) means that f(x) is continuous at all, but a finite number of points in (a, b).

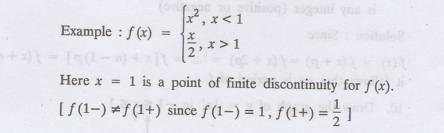
§ ADVANTAGES OF FOURIER SERIES :

1. Discontinuous function can be represented by Fourier series, although derivatives of the discontinuous functions do not exist. (This is not true for Taylor's series).

2. The Fourier series is useful in expanding the periodic functions, since outside the closed interval, there exists a periodic extension of the function.

3. Expansion of an oscillating function by Fourier series gives all modes of oscillation (fundamental and all overtones) which is extremely useful in physics.

4. Fourier series of a discontinuous function is not uniformly convergent at all points.

5. Term by term integration of a convergent Fourier series is always valid, and it may not be valid if the series is not convergent. However, term by term, differentiation of a Fourier series is not valid if the series is not convergent.