Transforms And Partial Differential Equations: UNIT III: Application Of Partial Differential Equations
Classification Of Partial Differential Equations
Examples
Let a second order p.d.e. in the function u of the two independent variables x, y be of the form
CLASSIFICATION OF PARTIAL DIFFERENTIAL
EQUATIONS
Let a second order p.d.e. in the
function u of the two independent variables x, y be of the form
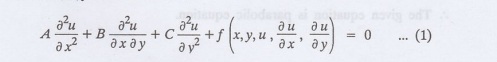
Equation (1) is classified as
elliptic, parabolic or hyperbolic depending on
B2-4AC < 0 (elliptic
equation)
B2-4AC = 0 (parabolic equation)
B2-4AC > 0
(hyperbolic equation)
Example

Problems
on classification of partial differential equations
Example
3.1.1 Find the nature of the partial differential equation 4Uxx + 4
Uxy + Uyy + 2 Ux - Uy = 0
Solution:
Given: 4uxx + 4uxy + uyy + 2 ux − uy
= 0

Example
3.1.2 Classify uxx +uyy = (ux)2+(uy)2

.. The given equation is elliptic
equation.

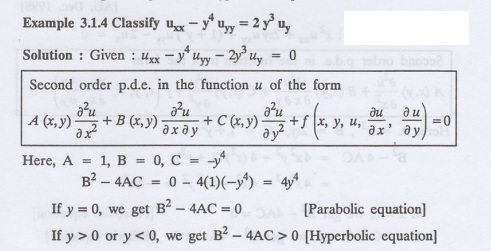
Example 3.1.5 Classify the p.d.e.
(1 + x)2 uxx- 4xuxy + uyy


Transforms And Partial Differential Equations: UNIT III: Application Of Partial Differential Equations : Tag: : Examples - Classification Of Partial Differential Equations